3 Bias circuits

3.1 Introduction

In the previous chapter, two components with larger-than-unity power gain were reviewed: the bipolar junction transistor (BJT) and the MOS-transistor. Both types of transistors are strongly non-linear, while the controlled output current only flows in one direction.

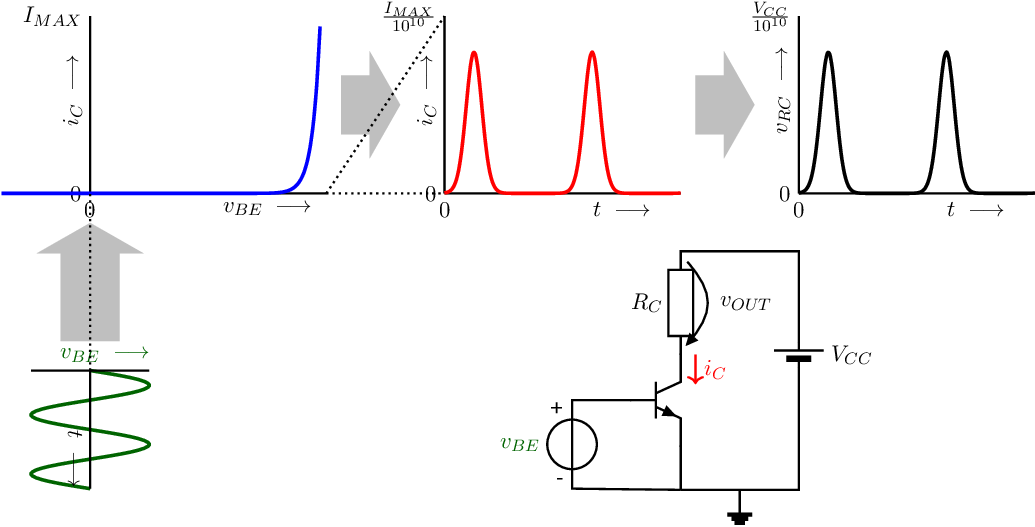
A very basic voltage amplifier is shown in Figure 3.1. In this circuit schematic, the (sinusoidal) input voltage with in this example a magnitude of about $150\mathit{mV}$ is applied to the NPN’s base-emitter port, while the resulting $i_C$ is converted to a voltage drop across resistor $R_C$. In equation:

Clearly the output current is not a sine: it is heavily distorted and the NPN’s collector current is very low as is the voltage across $R_C$. This is also illustrated by the signals in Figure 3.1. In the graphs in this Figure, $I_{\mathit{MAX}}$ is defined as $I_{\mathit{MAX}}=V_{\mathit{CC}}∕R_C$.

In this figure, the input voltage (as a function of time) is shown in the lower left corner. Note that this graph is rotated, having the x-axis (time axis) pointing downwards. The resulting collector current $i_C$ can easily be constructed by mirroring the input signal in the non-linear $v_{\mathit{BE}}-i_C$-curve shown in the left upper corner. This yields the $i_C(t)$ graph. Note that the y-axis of this graph is heavily zoomed with respect to the y-axis of the $v_{\mathit{BE}}-i_C$ graph is order to see the current. The rightmost graph in Figure 3.1 shows the voltage across $R_C$ as a function of time; this voltage is simply $v_{\mathit{RC}}=R_C\cdot i_C$. Note that this graph’s y-axis displays just a tiny bit of the supply voltage $V_{\mathit{CC}}$ in order to see any voltage. Note again that $i_C$ and $v_{\mathit{RC}}$ are very small and are far from sinusoidal: they are heavily distorted.

The very small magnitudes of $i_C$ and $v_{\mathit{RC}}$ in Figure 3.1 can be increased by increasing the input signal’s amplitude, but this causes an even more distorted $i_C$ and $v_{\mathit{RC}}$ that do have larger amplitudes. Figure 3.2 shows the situation in Figure 3.1 but with a 2.5 times larger input voltage.

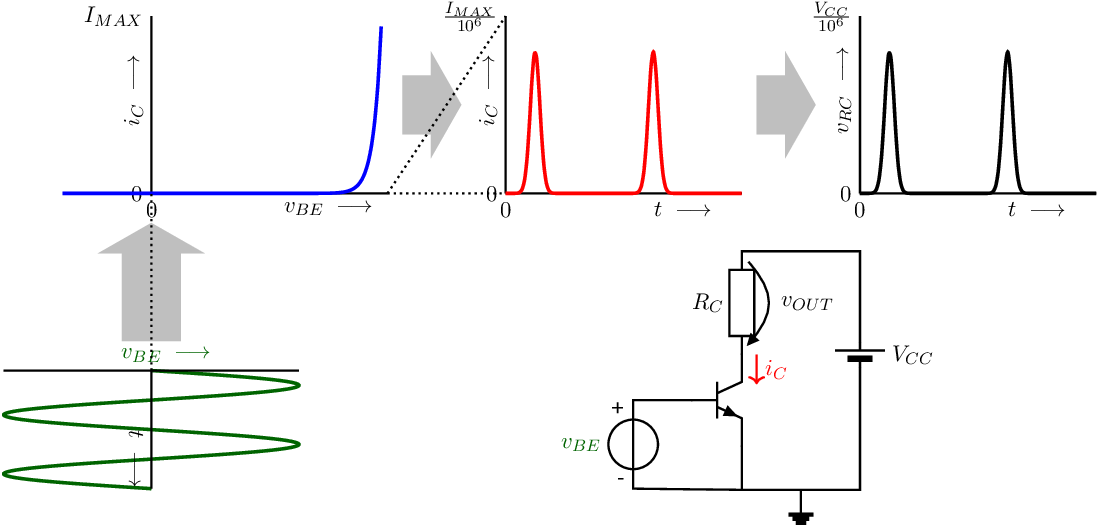
The main problem with this amplifier circuit is that its input signal goes positive and negative — where the transistor is mainly off during the majority of the input voltage — which translates into the rather small and heavily distorted output current. Proper biasing of transistors can solve this, and is the subject of the current chapter.

3.2 Biasing a transistor: the bias point

As a starting point for properly biasing a transistor, again the simple amplifier circuit of Figure 3.1 is assumed. For the principle however, it makes no difference whether we choose a different configuration or whether we would use a MOS transistor, vacuum tubes or something else with electrical power gain larger than 1. The general principle of such circuits is:

• the output current of the transistor is a non-linear, monotonous function of its input voltage.
• variation in output current due to an input voltage is (usually) converted into a varying output voltage by a resistor or some other impedance.

For transistors (and alike) there are two other (very much related) properties that yield requirements on proper biasing:

• the transistor’s output current can not change its sign: the current flows in just one direction.
• the transistor’s output current is (close to) zero if the input voltage is below a certain level (for NPNs, NMOS transistors, vacuum tubes, ...) or above a certain level (for PNPs, PMOS transistors, ...)

From this, it follows that to amplify an input signal with some degree of linearity,

• the voltage driving the transistor should be such that the transistor always conducts a significant collector or drain current.
• the voltage driving the transistor must be small, in order not to result in large distortion levels. This is usually satisfied if the variation in collector or drain current due to the variation in applied voltage is relatively (to the average current) small.

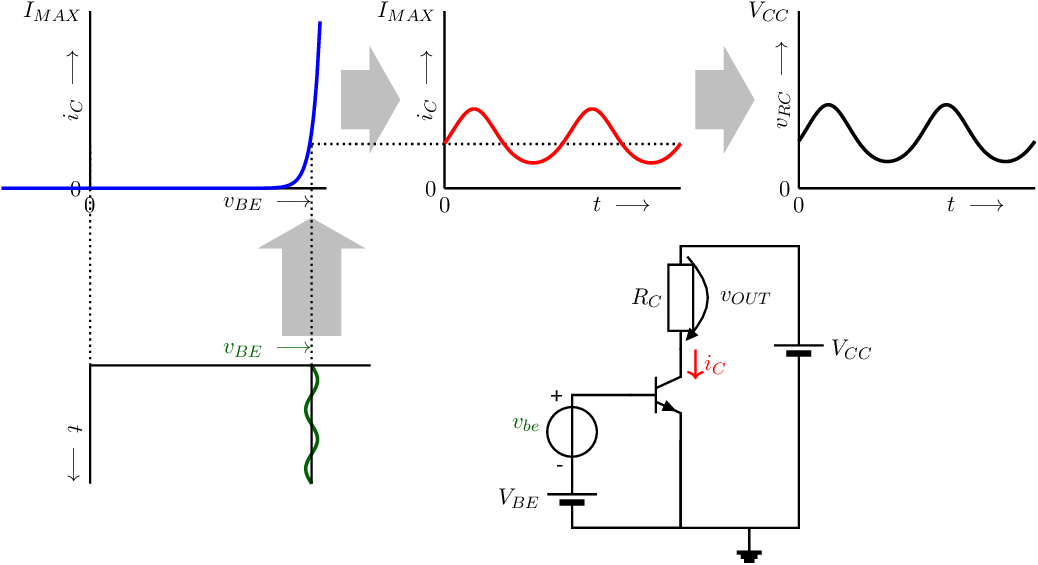
This preprocessing can be achieved by superimposing the input voltage variation (that can go positive and negative) on a larger DC-voltage and ensuring only a small relative current variation. The DC-voltage or its corresponding DC-current is called the bias point, operating point or quiescent point of the transistor. Figure 3.3 shows a Common Emitter Circuit (CEC, see chapter 5) that is biased in such a convenient bias point. In Figure 3.3 the input signal is a factor 10 smaller compared to the situation in Figure 3.1, although the output current is significantly larger and the circuit now works considerably more linear (actually: less non-linear). Note that the graphs in Figure 3.3 do not use scale factors for the current and voltage axes in the rightmost two graphs.

3.3 Biasing a transistor: requirements for its bias point

There are a number of requirements for a proper bias point of transistors in circuits. Because the output current of a transistor is a well defined monotonous function of its input voltage, it does not matter whether the bias point is defined in terms of driving voltage or output current. For a proper and stable bias:

1.

there must be a non-zero bias current through the transistor;

2.

the bias current must be as insensitive as possible to variations in temperature;

The circuit must operate properly for varying temperatures. Variations in temperature are usually due to the environment and the dissipation in the electronic component itself. If the temperature changes, the collector current (for a BJT) or the drain current (for a MOS transistor) changes significantly for a fixed input voltage ($V_{\mathit{BE}}$ respectively $V_{\mathit{GS}}$). A suitable bias circuit decreases this sensitivity to temperature significantly.

3.

the bias current has to be as insensitive as possible for the spread in characteristics of the transistor;

When producing electronic components there is always some spread in the components due to tolerances in the production process²⁵ . For example the spread in current gain of a bipolar transistor can amount to 50%; the spread of $I_{C0}$ is also significant. In MOS-transistors, the spread is mainly in the threshold voltage $V_T$ and in the current factor $K$.

4.

the bias current must be such that the input signal will be amplified sufficiently linearly.

The input signal of a transistor appears as a variation around the bias point. Hence, the bias point has to be chosen in such a way that the signal is amplified in a sufficiently linear fashion. Usually, this means that the current variations have to be small compared to the bias current²⁶ .

3.4 Biasing a transistor

Due to plain physics, the output current of a transistor cannot change sign and hence, to avoid high distortion levels or even clipping, a transistor must be biased at a bias current that is larger than the maximum desired current variation. Translated to the “input” of the transistor, this is equivalent to biasing the transistor with an input voltage ($V_{\mathit{GS}}$ or $V_{\mathit{BE}}$) that is larger than the signal voltage variations superimposed on it.

The bias current is set by applying a well-defined bias voltage to the transistor. Since a BJT also has a well-defined relation between the base and collector current, a bias current for a BJT can also be set using a bias base current. Concluding, we can bias a transistor by:

• BJT: setting $V_{\mathit{BE}}$
• BJT: forcing $I_C$, hence indirectly setting $V_{\mathit{BE}}=\frac{\mathit{kT}}{q}\mathit{ln}\left(\frac{I_C}{I_{C0}}\right)$.
• BJT: forcing $I_E$, hence indirectly setting $V_{\mathit{BE}}$, using also $I_E=\frac{{\beta }_{\mathit{fe}}+1}{{\beta }_{\mathit{fe}}}{I}_C$.
• MOS: setting $V_{\mathit{GS}}$
• MOS: forcing $I_S$ (and hence forcing $I_D$)

For sufficiently linear behavior, the variations on the transistor’s input voltage must be sufficiently small. The other way around: for small input voltage variations, the transistor’s operation is quite linear, and normal linear circuit analysis techniques may be used for evaluation of its (modelled) behavior²⁷ .

In this chapter, we describe the methods for obtaining a well defined bias point. In chapter 4, a linear equivalent circuit for transistors is derived that describes its behaviour about the bias point, and in chapter 5 we give some examples of amplifier circuits, where the small-signal equivalent circuits of chapter 4 are applied.

3.5 Biasing a BJT

Before we go into the details on how to bias a BJT, it might be useful to recap the element equations:²⁸

As stated in §3.4, there are many methods for biasing a BJT that essentially boil down to forcing a certain bias current $I_C$ and its corresponding bias voltage $V_{\mathit{BE}}$.

3.5.1 Biasing $V_{\mathit{BE}}$ using a DC-voltage source

The easiest method for forcing a collector current is using a DC-voltage source that provides a $V_{\mathit{BE}}=\frac{\mathit{kT}}{q}\mathit{ln}(I_C∕I_{C0})$, as in Figure 3.3. and in Figure 3.4a. For transistors that have to deliver a DC current this is quite sufficient provided that the DC-voltage can be set sufficiently accurate and provided that for the transistor’s operation on signals, the $V_{\mathit{BE}}$ does not have to change. This latter is usually not satisfied.

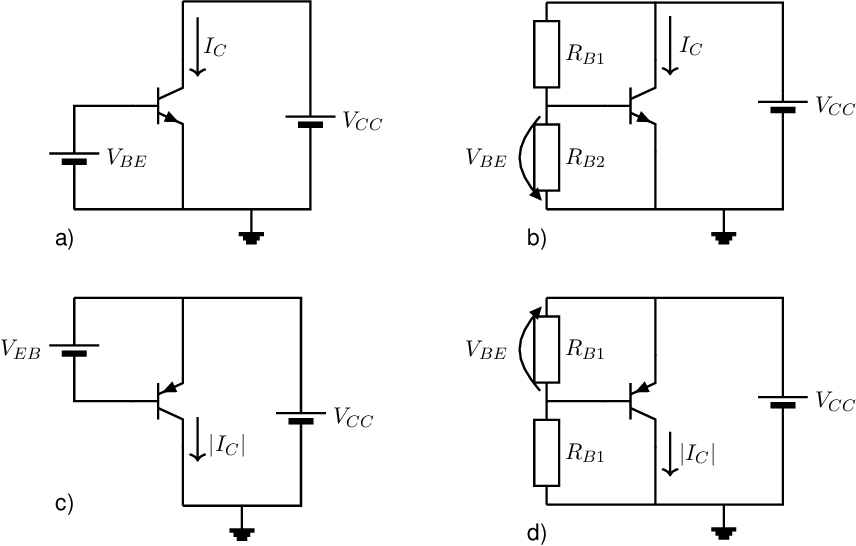
Another disadvantage of this method is that it is rather sensitive to variations in temperature due to the temperature dependence of the BJT. It can be derived that typically 1 K increase in temperature already results in an increase in $I_C$ of about 7%²⁹ . However, an advantage is that the base current drops out of the equation which means that the circuit is insensitive to variations in current gain ${\beta }_{\mathit{fe}}$.

An alternative to the circuit in Figure 3.4a is the implementation (with relatively low ohmic resistors) in Figure 3.4b.

3.5.2 Biasing by forcing a base current (ideal)

Bipolar transistors can be biased to a certain DC-current in various ways. When the current gain ${\beta }_{\mathit{fe}}$ is known, the easiest way is to “force” a DC-base current $I_B$, which results in a DC-collector current $I_C={\beta }_{\mathit{fe}}\cdot I_B$. From a fundamental point of view, forcing a base current $I_B$ has to be done using a current source, as shown in Figure 3.5a.

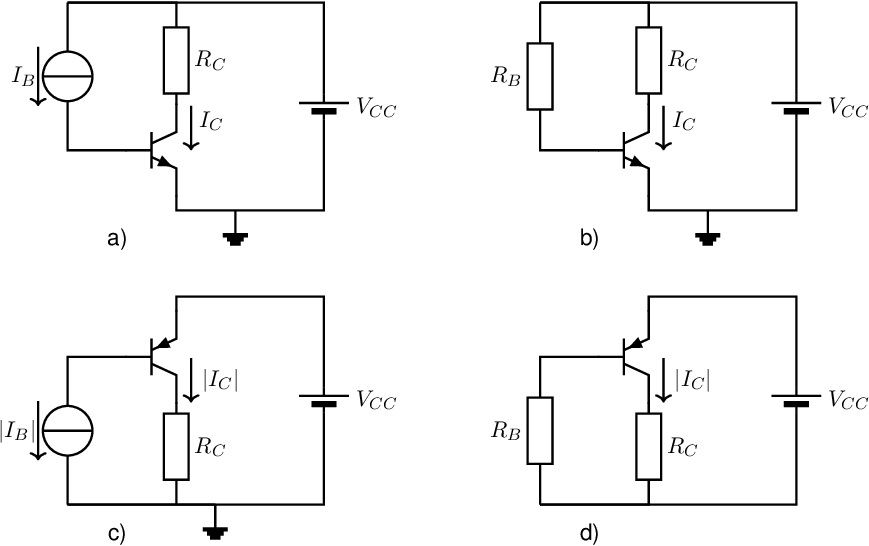
Theoretically, this is a good method to set a bias $I_C$ as long as the current gain factor ${\beta }_{\mathit{fe}}$ of the BJT is known and is sufficiently constant. This ${\beta }_{\mathit{fe}}$ is reasonably insensitive to variations in temperature, but can vary significantly between BJTs.

3.5.3 Biasing by forcing a base current (non ideal)

Using ideal current sources to bias BJTs is fairly easy, but also purely theoretical. In reality, there is no such thing as an ideal current source: they are always composed of passive (R, L, C, ...) and/or active (MOST, BJT, ...) components. Provided that the output impedance of such a circuit is very high — compared to the impedance of the BJT base-emitter junction’s impedance – the bias circuit may be modelled as an ideal source.

In many circuits, the ideal current source of Figure 3.5a is implemented with a quite simple highly non-ideal current source: a resistor, see 3.5b. The value of $I_B$ is set by selecting an appropriate value for resistor $R_B$. Using the brute force approach a suitable $R_B$ is easily derived assuming that $V_{\mathit{BE}}$ is known:

For synthesis applications — where you determine the behavior — $V_{\mathit{BE}}$ can easily be expressed in the target $I_C$ that you want to set as bias condition if you know the element equation including its constants. Then you can directly calculate the required value $R_B$. No problem.

For synthesis applications where you do not know all BJT parameters $V_{\mathit{BE}}$ cannot be expressed in the target $I_C$... some parameters are missing. Then there is no way to exactly calculate the required value $R_B$. Using a smart trick — or a fair assumption — the calculations can be done.

For analysis, where you are given $R_B$ and may be asked to calculate $I_C$ this is a major problem. In that case you would have to solve $I_C=\frac{{\beta }_{\mathit{fe}}\cdot (V_{\mathit{CC}}-V_{\mathit{BE}}(I_C))}{R_B}$ which is very hard since it involves solving an equation including an exponential relation and at least one linear relation. Although that may seem easy to solve, it actually is quite nasty, near impossible. Using that same smart trick — or a fair assumption — also these calculations can be done.

A good assumption or model (in terms of accuracy and simplicity) is that the $V_{\mathit{BE}}$ of a silicon bipolar transistor at room temperature is typically between 0.6 V and 0.7 V. This stems from some physical properties of silicon and from the fact that due to the exponential $I_C-V_{\mathit{BE}}$ relation for every change in $V_{\mathit{BE}}$ by only $18\mathit{mV}$ the current changes by a factor 2. For a change in $V_{\mathit{BE}}$ by $60\mathit{mV}$ the collector current then changes a factor 10. The other way round, for any sensible current the $V_{\mathit{BE}}$ for silicon BJTs ends up between 600mV and 700mV. If you really stress the transistor it may be as high as 800mV. Consequently, a fair estimation for $V_{\mathit{BE}}$ for silicon BJTs is:

Although the choice of $V_{\mathit{BE}}\approx$ 0.65 V seems arbitrary, it does give a result with reasonable accuracy:

• if the source voltage $V_{\mathit{CC}}$ is relatively large, $V_{\mathit{BE}}<<V_{\mathit{CC}}$, then an error in the assumption on the value of $V_{\mathit{BE}}$ will have a small effect on the bias current of the BJT.

• the voltage $V_{\mathit{BE}}$ varies just a little with collector current, due to the logarithmic dependency (with scale factor $\mathit{kT}∕q$). For e.g.

  • a 20% error (or change) in collector current, $\mathrm{\Delta }{V}_{\mathit{BE}}=\pm 5\mathit{mV}$,
  • an error (or change) of a factor 2 in $I_C$ corresponds to a $\mathrm{\Delta }{V}_{\mathit{BE}}=\pm 18\mathit{mV}$,
  • a factor 10 off in current corresponds to 60mV difference in $V_{\mathit{BE}}$.

It can be concluded that if the BJT is biased properly, the errors introduced by the assumption $V_{\mathit{BE}}\approx 0.65V$ are usually small, while the calculations are simplified enormously. If you do not like the 0.65 V, please use 0.7 V or some other easy-to-use number in that (silicon) ballpark.

Advantages of setting a bias current using a base-series-resistor include:

• only one resistor value is to be determined.
• the temperature sensitivity of ${\beta }_{\mathit{fe}}$ is usually low
• it is quite stable: if $I_C$ were to increase (and then $I_B$ as well) for some reason, then the voltage drop across $R_B$ will increase, causing $V_{\mathit{BE}}$ to decrease. This way a kind of self-stabilising biasing is obtained.

A disadvantage is the large sensitivity to spread in ${\beta }_{\mathit{fe}}$. For unselected discrete transistors of one production series, the value of ${\beta }_{\mathit{fe}}$ can vary up to 50%, which means that for every new transistor, a different resistor value must be set to get the same $I_C$. In a production facility this would be a huge problem while it is not in a laboratory (as long as you do not change the transistor). A possible solution for this spread sensitivity is introduced in the next section.

3.5.4 Biasing using emitter degeneration

The main disadvantage of the bias methods introduced above is that sensitivities to component spread, having inaccurate component values, temperature fluctuations, ... is significant. These disadvantages can be mitigated using some form of “self-correction”, which is applied in just about every real circuit. This self-correction assures that variations are counteracted by the circuit itself. There are many different methods for self-correction³⁰ . The general term for these effects is feedback. In other chapters in this book, feedback is explained in detail. For now, we use relatively simple feedback configurations.

In feedback circuits, the measured quantity is compared to the desired value, then (in this chapter) this measured difference is used to minimize the difference between the two. For a transistor circuit, we could for instance measure the output (collector or drain) current and use this measured quantity to get and keep this current at a specific value. This leads to 2 possibilities to implement feedback:

• the output current of a BJT can be measured at the collector or emitter (for a MOS transistor at the source or at the drain).
• the $V_{\mathit{BE}}$ is changed as to approach the target $I_C$.

A third method is to measure the $I_B=I_C∕{\beta }_{\mathit{fe}}$ and adjust the $V_{\mathit{BE}}$ to obtain the target $I_B∕{\beta }_{\mathit{fe}}$; this method assumes that the ${\beta }_{\mathit{fe}}$ is sufficiently accurately known. Figure 3.6 shows these three methods. Note that these methods depict simplified situations for circuits with one transistor where (a measure for) the collector current $I_C$ is used to adjust the transistor’s $V_{\mathit{BE}}$ in order to get a stable and well defined bias current $I_C$. The principle can be generalized to feedback around an arbitrary system.

An often used feedback method measuring the bias current at the emitter (or source) side is called emitter degeneration (or source degeneration for a MOS transistor). In Figure 3.7, this emitter degeneration is shown for an NPN transistor. The circuit counteracts variations in the bias current ($I_C$ and/or $I_E$) due to e.g. temperature changes, component spread, ageing, and much more.

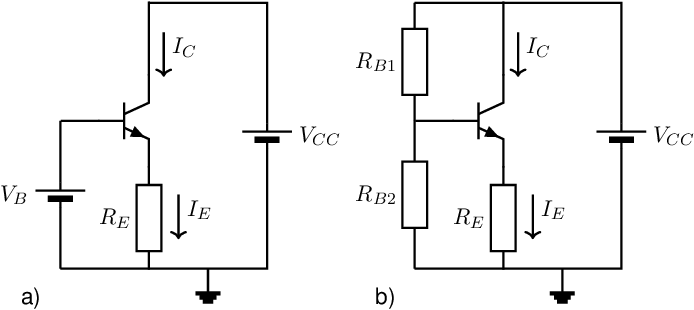
Let’s assume — for illustration purposes — that the temperature of the transistor increases. Due to some the semiconductor physics that determines the behavior of the BJT, for a constant $V_{\mathit{BE}}$ the transistor’s $I_C$ and $I_E$ increase with about 7%/K. With the circuits shown in 3.7, this increasing $I_E$ results in an increase of the voltage drop across $R_E$. Assuming — for simplicity — a constant base voltage $V_B$, the increasing emitter voltage $V_E$ results in a decrease of $V_{\mathit{BE}}$ which counteracts the initial increase of the $I_E$ and $I_C=I_E\cdot \frac{{\beta }_{\mathit{fe}}}{{\beta }_{\mathit{fe}}+1}$.

In the circuit of Figure 3.7a, the collector current of the BJT is set by applying a base voltage, and using emitter-degeneration (feedback via the emitter current and emitter voltage). Synthesizing or dimensioning a circuit — forcing the circuit to do what you want it to do — can be done in an exact way:

where $I_C$ is the bias current. for the BJT For this, you have to know the element equations including the constants in it. If e.g. the $I_{C0}$ in the transistor’s element equation is unknown then you have to make assumptions, such as $V_{\mathit{BE}}\approx 0.65V$ in the derivation.

Note that implicitly this derivation assumes that there is a certain amount of feedback via $R_E$. If (in the previous equation) $V_B$ is chosen to be equal to the $V_{\mathit{BE}}$ required to get your target $I_E$ then the voltage drop across $R_E$ is zero, yielding $R_E=0$ and consequently then there is no feedback. It can be derived that to have significant feedback to get a stable operating point for an NPN or PNP

For analysis the resulting bias current now follows from some straightforward math:

This looks quite simple. It is however not a closed form expression as $I_C$ is on both sides of the equation. Solving this analytically can be done using the nasty Lambert-W-function, but that does not give insight or useful results. Using the previously introduced assumption that for a properly operating silicon NPN $V_{\mathit{BE}}\approx 0.65V$ and assuming that $R_E\cdot I_C>>\frac{\mathit{kT}}{q}$ for proper emitter degeneration:

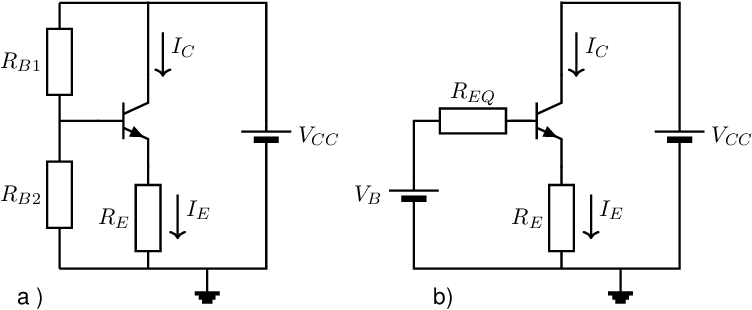
In Figure 3.7b the base voltage is set by resistors $R_{B1}$ and $R_{B2}$. If this voltage divider has a low impedance, then the base voltage is not (actually, hardly) a function of the base current. In that case $V_B=R_{B2}∕(R_{B1}+R_{B2})\cdot V_{\mathit{CC}}$, which gives effectively the configuration in Figure 3.7a.

If the voltage divider is not low ohmic, then the base current does have an effect on the base voltage. The bias current of this circuit can be calculated by using brute force, but it can be simplified using divide-and-conquer. In this case, using a Thévenin representation of the resistive divider and the voltage source simplifies things considerably. The resulting equivalent network is shown in Figure 3.8b with $V_{\mathit{EQ}}=V_{\mathit{CC}}\cdot \frac{R_{B2}}{R_{B1}+R_{B2}}$ and $R_{\mathit{EQ}}=R_{B1}∕∕R_{B2}$.

Then it can be derived that:

Note that now feedback is implemented via both $I_E$ and $I_B$ that both are related to $I_C$. Due to the ratio $({\beta }_{\mathit{fe}}+1)$ between $I_E$ and $I_B$ the impact of the feedback via $R_{B1}∕∕R_{B2}$ is however lower by a factor $({\beta }_{\mathit{fe}}+1)$ but typically $R_{B1}∕∕R_{B2}$ can be designed to be much more high-ohmic than $R_E$. Neglecting its sensitivity to variations in ${\beta }_{\mathit{fe}}$, operating point stabilizing feedback via $R_{B1}∕∕R_{B2}$, can also be a useful approach, as alternative or in combination with emitter degeneration. Note that this feedback is the highest for $R_{B2}\to \infty$ and can be made more efficient than feedback via $R_E$ if variations in ${\beta }_{\mathit{fe}}$ and $I_C(V_{\mathit{CE}})$ dependencies can be neglected.

3.6 Biasing a MOS-transistor

Almost everything derived so far for the BJT is also applicable to the MOS-transistor. The only exception is the stabilizing feedback via $R_{B1}∕∕R_{B2}$ as shown in Figure 3.8 - this does not work for MOS-transistors as there is no relation between $I_D$ and $I_G$ in MOS transistors as the latter current is (ideally) zero.

Here we again limit ourselves to the N-channel enhancement MOS transistor (having $V_T>0$ and hence is off for $V_{\mathit{GS}}=0$). For applications in amplifier circuits, the MOS transistor is usually biased in saturation, causing the drain current to depend only — as a good approximation — on the gate-source voltage, not on the drain-source voltage:

The bias current $I_D$ can be set by a proper $V_{\mathit{GS}}$ using a voltage source. The main problem with biasing using a voltage source is — just like with the BJT — that variations (i.e. the signal that has to be amplified) are hard to superimpose. Therefore, usually the bias is set by means of a voltage divider from the supply voltage, as shown in Figure 3.9.

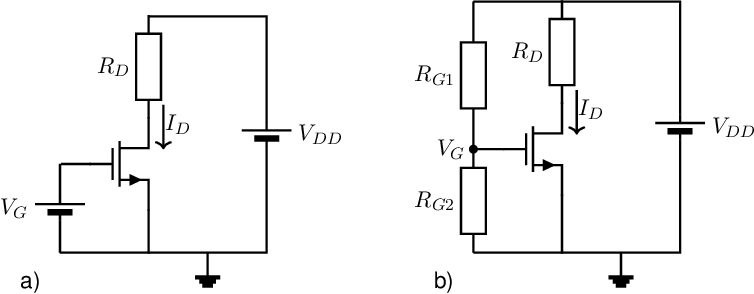
The MOS-transistor is, just as a diode and BJT, sensitive to changes in temperature. For example, the threshold voltage $V_T$ has a temperature coefficient roughly equal to $-1{\mathit{mV}\cdot K}^{-1}$. In the $K$-factor, the carrier mobility $\mu$ has the largest temperature dependence, which is about proportional to T${}^{-2}$. The change in threshold voltage causes $i_D$ to rise with increasing temperature, while the decrease of the $K$-factor tends to decrease $i_D$. Furthermore, the parameters $K$ and $V_T$ spread from transistor to transistor. Using the same feedback method as for the BJT, here using source degeneration, their influence can be limited.

3.6.1 Biasing using source degeneration

Earlier in this chapter, it was shown that the bias point of a BJT could be made much less sensitive for all kinds of variations by using feedback. For the BJT, this is usually implemented by an emitter-series resistor: using so-called emitter degeneration. For the MOS transistor the same can be done, yielding the so-called source degeneration.

The effect of a source degeneration is analysed briefly below, both graphically — using a load line construction — and in analytical. For both, the example circuit in Figure 3.10 is assumed.

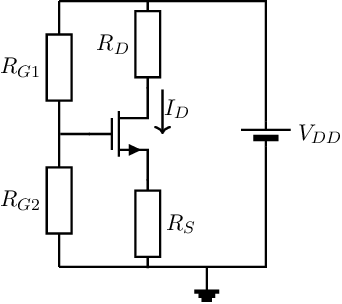
Using a loadline construction, the bias point (or solution) for a mesh can be obtained graphically. This holds fora mesh in a linear circuit and for a mesh in a nonlinear circuit. In this section, the $I_D$ in the circuit schematic in Figure 3.10 will be obtained, along with it sensitivities to (in this example) variations in $K$. A suitable mesh is then the one containing $R_{G2}$, $V_{\mathit{GS}}$ and $R_S$. Noting that the gate current is zero, this yields

With $R_S=0$ the transistor’s drain current is simply $I_D=\frac{1}{2}K{(V_{\mathit{GS}}-V_T)}^2$ and then any change in $K$ results in a proportional change in $I_D$. For a situation for which $K=2\mathit{mA}∕V^2$, $V_G=2.5V$ the loadline plot is shown in Figure 3.11.

The blue curved curve correspond to the $I_D(V_{\mathit{GS}})$ relations for the nominal $K$; those for $\mathit{K\prime }=K\cdot 0.7$ and for $\mathit{K\prime \prime }=1.3\cdot K$ are in red and green respectively. The”loadline for $R_S$ is the vertical line at $V_{\mathit{GS}}=2.5V$. The intersect of the vertical line and the curves mark the $I-V$-point where both the KCL and the KVL are satisfied. This is the graphically obtained solution of the set of equations listed earlier. For the (in this example) nominal $K$, $I_D=4\mathit{mA}$, the change in $I_D$ between the minimum $K$ and the maximum $K$ is 2.4 mA for the nominal $I_D=4\mathit{mA}$.

Aiming at a nominal current of 4mA — the same as above — but now using source degeneration, the load line plot changes. To be able to obtain the same $I_D$ for the same $V_G$ but using a non-zero $R_S$, the transistor must deliver that 4mA at a lower $V_{\mathit{GS}}$ which requires a larger $K$. Assuming $K_{\mathit{nom}}=8\mathit{mA}∕V^2$ and $R_S=250\mathrm{\Omega }$, and again $\pm 30\%$ spread in the $K$, the loadline plot as shown on the left in Figure 3.12 results. The I-V curve of $R_S$, on a $V_{\mathit{GS}}$ axis corresponds to the line from upper left to lower right. The bias I-V points correspond to the intersection of the resistor-I-V-curve and the transistor’s I-V-curves. Due to this source degeneration the variation in $I_D$ is reduced from $\mathrm{\Delta }{I}_D\approx 2.4\mathit{mA}$ to $\mathrm{\Delta }{I}_D\approx 0.82\mathit{mA}$.

Increasing the $R_S$ to get an even more stable bias point, the loadline plot as shown on the right hand side in Figure 3.12 results. For this plot, $K_{\mathit{nom}}=32\mathit{mA}∕V^2$ and $R_S=375\mathrm{\Omega }$, and again $\pm 30\%$ spread in the $K$ is included. Now, due to this higher source degeneration the variation in $I_D$ is reduced to $\mathrm{\Delta }{I}_D\approx 0.35\mathit{mA}$.