Semiconductor physics in a nutshell

2 Semiconductor physics in a nutshell

2.1 Introduction

This chapter presents a brief introduction into semiconductor physics and the behavior of the most important nonlinear electrical components: the diode, the bipolar junction transistor (BJT) and the MOS-transistor. At the end of this chapter you should have a basic understanding of the operation of semiconductor components. The theoretical underlying physics and other in depth stuff is outside the scope of this book.

Non-linear components¹⁴ are required in any system that:

performs nonlinear functions. This could be anything: translating analog signals to digital signals, frequency conversions in transmitters and receivers, or digital functions. Almost every serious electronic system needs nonlinear components to function properly.
requires power gain larger than 1. Power gain is used to boost small signals to a sufficient power level, but is also essential to compensate for signal losses in a system.

In components with power gain (larger than 1) usually a large output power is controlled by a much smaller input power. The difference in output power and input power (and dissipated power!) is supplied by some energy source, which usually is a DC current source or DC voltage source: at $0 Hz$ . Because the frequency of the DC sources is in general very different from the frequency of the signal to be amplified, frequency conversion is necessary. Since frequency conversion is not possible with only linear components, every amplifier with more-than-unity power gain requires nonlinear components.

The electrical conductance of any material is determined by both its lattice structure and by some properties of the atoms in the lattice. In semiconductor physics typically a nice regular lattice is assumed. Then the electrical properties of the material are completely determined by the atoms, or more specifically by the band structure of the atoms in the lattice.

An atom consists of a nucleus, surrounded by bands, each of which can contain a specific number of electrons. Now, the following situations can be distinguished:

The $m$ bands closest to the nucleus are completely filled with electrons, while all other bands are completely empty. In the full bands, electrons have no place to go, while in the empty bands, there are no electrons to move around. In this case, there is no possibility for electrons to move through the lattice and thus the electrical current is 0 A. Materials with this property are called insulators.
The $m$ bands closest to the nucleus are completely filled with electrons, while the ${(m + 1)}^{th}$ band is neither full nor empty. Just like in the case for insulators, electrons in full bands can not move through the lattice. However, in the partially filled ${(m + 1)}^{th}$ band electrons can move. Even if there is only one electron free to move per atom, there is a huge amount of electrons that can move around already in very small volumes of semiconductor material. These electrons can move freely through the entire lattice; these materials are conductors.
The $m$ bands closest to the nucleus are virtually completely filled with electrons, while the first band that isn’t completely filled is almost empty. Not completely empty, but almost empty. Effectively this means that just 1 electron per many atoms can move around in the lattice. This is the case in what are called semiconducting materials. Semiconducting materials have very nice properties that can be used to create nonlinear components. In the next section, these materials are explored in more detail.

2.2 Semiconductors

From an electrical point of view, most of the bands in an atom are not very interesting:

completely filled bands are full. Electrons cannot move anywhere simply because there is no place for them to move to. These bands thus do not contribute to the electrical conductance.
completely empty bands don’t contain any electrons and thus do not contribute to the conductance either.

Therefore, from now on, we only consider the two outermost bands of a (semi)conductor that contain electrons. The outermost of the two is denoted as conduction band, while the inner of the two is called the valence band.

In any semiconductor, the valence band can hold (per atom) as many electrons as there are electrons available for this band: the valence band can hence be filled exactly. If this is the case then there are no electrons left for the conduction band, which thus remains completely empty. The semiconductor now acts as an insulator.

The nice thing about semiconductors is that the valence band and conduction band are close to each other, making it possible for electrons in the valence band to gain enough (thermal or electrical) energy to “jump the gap” to the conduction band. Once these electrons are in the conduction band, they may lose energy and fall back into the valence band¹⁵ .

pict — Figure 2.1: Atomic structure of a semiconductor (here Si in a mono crystalline solid state lattice): the 1s, 2s, 2p and 3s bands can be completely filled and the 3p band then is empty. The 3s and 3p bands are sufficiently close that some electrons can ‘evaporate’ to the conduction band at room temperature.

Once an electron has evaporated from the valence band, across the band gap to the conduction band, it has an enormous amount of space to move around freely: such an electron (negative charge) can contribute to the electrical conduction. At the same time, that electron leaves a void behind in the valence band, which is denoted as a hole. The charge of a hole is positive: it corresponds to missing one electron. The hole can also contribute to the electrical conduction. Note that moving a hole through a lattice is due to subsequent moving electrons into that hole: the hole moves therefore in the opposite direction of the electrons!

Because the movement of a hole is due to subsequent movements of different electrons, one might already guess that the electron in the conduction band can move easier than the hole in the valence band. The ease of moving through the lattice for both the electron (negative charge carrier) and the hole (-electron, positive charge carrier) are usually described by its mobility. The mobility tells you how much speed (m/s) you can get in some electrical field (V/m), making the unit of mobility $m^{2} ∕ (V \cdot s)$ , or more commonly used in the field of semiconductors $c m^{2} ∕ (V \cdot s)$ . In silicon the mobility of holes is about a factor 2 or 3 or $e$ lower than that of electrons.

The most commonly used semiconductor is silicon (Si), whose valence and conduction bands each can hold 4 electrons per atom if it is in a mono crystalline solid state. Since it is a ‘group IV’ atom in the periodic table it has 4 electrons available for those 2 bands. The distance between the conduction band and valance band is such that at room temperature a few electrons in the valance band can get enough energy to jump into the conduction band: it is a semiconductor¹⁶ .

Semiconductor materials with only one flavor of atoms are boring and not very useful. This is why we use doping to make multiple favours of doped semiconducting material.

In undoped — or intrinsic — semiconductors, the number of electrons in the conduction band equals the number of holes in the valence band, since both are caused by the same ‘evaporation’ process. This number of holes and electrons is low, and consequently intrinsic silicon shows low conductivity (at and around room temperature).
If a small number of original ‘group IV’ atoms are replaced by ‘group III’ atoms, there will be too few electrons in the valence band. In other words, even without any ‘evaporation’ there will be holes in the valence band that can move freely through the lattice. Since holes are positive charge carriers, we call this a P-type semiconductor.
If a small number of original atoms is replaced by ‘group V’ atoms, there will be more electrons than can fit the valence band: these electrons can only find a place in the conduction band, where they can move freely, through the lattice because of all the space there. Because electrons have negative charge, this kind of material is called an N-type semiconductor.

2.3 Diodes

Electrons flow from a lower potential to a higher potential, whereas holes move in the opposite direction, towards lower potential. This seems strange, but it is because at around 1900 A.D. some guy defined this the wrong way and now we have to deal with that forever.

Now, assuming a semiconducting lattice, one half of which is N-doped (excess electrons) and the other half having P-type doping atoms (excess holes), then:

a large current (of holes and electrons) can flow if the N-doped side has a lower potential than the P-doped side: there are a lot of electrons in the N-region that can (and will) flow to a higher potential, and there are lots of holes in the P-region that can (and will) flow to a lower potential.
electrons and holes will stay where they are if the polarity is reversed: electrons are already at the higher potential at the N-doped side and likewise the holes at the P-doped side are already at the lowest potential. None of these carriers is inclined to move. Only the few holes in the N-type region that are due to ’evaporation’ of electrons to the conduction band (and the few electrons in the P-doped region) flow in this case. As there are just few of these charge carriers, the resulting current is quite low.
using equations for drift and diffusion, it can be derived that the actual voltage-current relation of the diode is:

$\begin{array}{rcl} i_{D} & = & I_{D 0} \cdot (e^{\frac{q \cdot v_{D}}{k \cdot T}} - 1) \end{array}$

where $I_{D 0}$ depends on the semiconductor material, dopant levels, size, and is very much temperature dependent. Further, $q$ is the elementary charge, $k$ the Boltzmann constant and $T$ is the absolute temperature. The factor $v_{D}$ is the voltage applied across the P-N-structure.

Such a component is usually called a pn-junction or diode. In a diode, there can hence be two major current components (and two minor ones that make up the leakage current and that are neglected here): an electron current from n to p and a hole current component from p to n, if the potential at the p-side is higher than that on the n-side. Both of these major current components contribute to a conventional current (in Ampère) in the same direction: from p to n, since electrons and holes are oppositely charged and flow in opposite directions.

2.3.1 Temperature dependency of the diode current

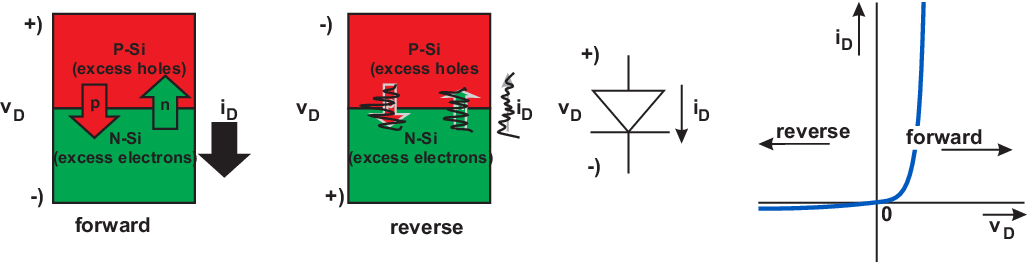
It was stated earlier that the diode current-voltage relation in a quite-a-lot simplified case is

\begin{array}{rcl} i_{D} & = & I_{D 0} \cdot (e^{\frac{q \cdot v_{D}}{k \cdot T}} - 1) . \end{array}

One might be tempted to think that the only temperature dependency is due to the term between brackets, that includes the absolute temperature $T$ . Due to this term alone, at constant $v_{D}$ the diode current would decrease with increasing temperature $T$ . However, the factor $I_{D 0}$ in this relation is actually also heavily temperature dependent and increases with increasing temperature $T$ . A (still simplified) relation for $I_{D 0}$ including material properties and sizes is:

\begin{array}{rcl} I_{D 0} & = A \cdot q \cdot (\frac{D_{p}}{L_{p}} \frac{n_{i}^{2}}{N_{D}} + \frac{D_{n}}{L_{n}} \frac{n_{i}^{2}}{N_{A}}) \\ where: \\ A is the cross section area of the junction \\ D_{p} and D_{n} are the diffusion constant for holes and electrons in the semiconductor material \\ L_{p} and L_{n} are the carrier diffusion lengths for holes and electrons in the semiconductor \\ N_{D} and N_{A} are the dopant levels in the n-region and in the p-region \\ n_{i} is the intrinsic carrier concentration \end{array}

Especially this $n_{i}$ is quite temperature dependent. It depends on the so-called density of states, the material bandgap and on thermal energy. In equation this translates into

\begin{array}{rcl} n_{i}^{2} & = C \cdot {(kT)}^{3} e^{- \frac{W_{g}}{kT}} \\ where & C is a material dependent constant \\ W_{g} the bandgap \\ T the temperature [K] \end{array}

An expanded version of the voltage-current relation of a diode, including temperature effects, would be

\begin{array}{rcl} i_{D} & = & A \cdot q \cdot (\frac{D_{p}}{L_{p}} \frac{1}{N_{D}} + \frac{D_{n}}{L_{n}} \frac{1}{N_{A}}) \cdot C \cdot {(kT)}^{3} e^{- \frac{W_{g}}{kT}} \cdot (e^{\frac{q \cdot v_{D}}{k \cdot T}} - 1) . \end{array}

The combination of the various exponential terms in this (expanded version of) $i_{D}$ in combination with $T^{3}$ results in a diode current that (at constant $v_{D}$ ) increases about exponentially with temperature around room temperature. As a rough guideline, the diode current (at constant diode voltage) doubles for every 10K increase in temperature. The other way around, at a constant diode current, the diode voltage decreases about 18mV with a 10K increase in temperature.

2.3.2 Capacitive effects in junctions: in reverse

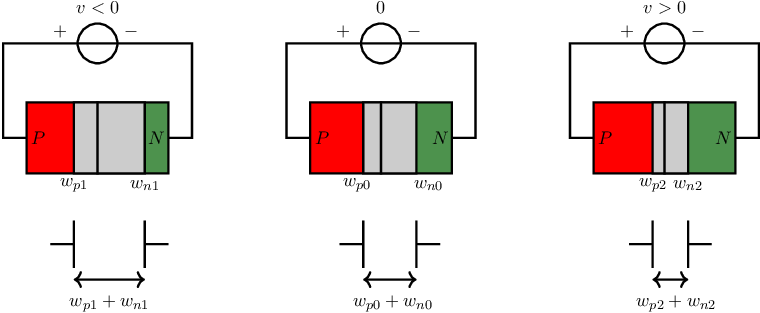
As argumented in §2.3, holes from the P-doped part in a junction diffuse towards the N-doped region, and vice versa. Being initially unchanged materials, after diffusion of mobile charge carriers, in both the P-region and the N-region ionized atoms are left behind. These ionized atoms form a so-called depletion layer around the metallurgical junction where (nearly) all atoms are ionized. In this layer, the charge is associated with the ionized atoms and hence are not mobile. The amount of depletion charge is a function of the applied voltage, and can be written as $Q_{depletion} (v_{D})$ . Because the charge is dependent on the applied voltage, we now can define a (non-linear) depletion capacitance

C_{depletion} (v_{D}) = \frac{\partial Q_{PN} (v_{D})}{\partial v_{D}}

Using in-depth semiconductor physics derivations, the exact $Q_{depletion} (v_{D})$ can be calculated. Using the fact the the charge is (almost entirely) stored as ionized atoms, it can be derived that the width of this depleted layer, assuming uniform dopant density in the P-region and in the N-region is

w_{depletion} (v_{D}) = w_{n} + w_{p} = \sqrt{φ_{o} - v_{D}} \sqrt{\frac{2 \cdot 𝜀_{o} 𝜀_{r} \cdot (N_{A} + N_{D})}{q \cdot N_{A} N_{D}}}

Here $φ_{o}$ is a the so-called built in voltage that depends on the (fixed) material and dopant levels and weakly depends on temperature. Noting that in the depletion layer there are almost no mobile charge carriers, a pn-junction is very similar to a plate capacitance where the plate distance equals the width of this depletion layer $w_{depletion} (v_{D})$ . This equivalence is depicted in the figure below:

The capacitance for a plate capacitor is given by :

C = \frac{A 𝜀_{0} 𝜀_{r}}{d}

(2.1)

where the distance between the plates is $d$ and the area of the plates equals $A$ . Using this to get the capacitance associated with a the depletion layer in a p-n junction, it follows that (assuming uniform dopant levels in both the N and P region)

C_{depletion} = \frac{A 𝜀_{0} 𝜀_{r}}{\sqrt{φ_{o} - v_{D}} \sqrt{\frac{2 \cdot 𝜀_{o} 𝜀_{r} \cdot (N_{A} + N_{D})}{q \cdot N_{A} \cdot N_{D}}}} = \frac{C_{0}}{\sqrt{1 - \frac{v_{D}}{φ_{0}}}}

For most dopant profiles, it can be shown that this relation can be rewritten into something like the following relation. Note that this presents a capacitance that depends on the material, the dopant level, depends weakly on temperature AND depends on the applied voltage.

C_{depletion} = \frac{C_{0}}{{(1 - \frac{v_{D}}{φ_{0}})}^{m}} \frac{1}{3} \leq m \leq \frac{1}{2}

2.3.3 Extra capacitive effects in junctions in forward

Operating a junction in forward, an appreciable forward current occurs already at a relatively low forward voltages. This current is due to diffusing majority carriers: holes from the P-region to the N-region and electrons from the N-region to the P-region. These current components are exponentially dependent on the applied voltage. The diffusing majority charge takes some time to diffuse from one side of the depletion layer to the other side, which can be modelled as an apparent charge storage effect: as a capacitance. Introducing a lifetime parameter $τ$ that models the time it takes for a charge carrier to diffuse, the total charge associated with forward currents is

Q_{diff} = I_{0} \cdot τ \cdot e^{\frac{q v_{D}}{kT}} ≅ I_{D} \cdot τ

(2.2)

and consequently the diffusion capacitance is

C_{diff} = \frac{\partial Q_{diff}}{\partial v_{D}} ≅ \frac{\partial I_{D} \cdot τ}{\partial v_{D}} = \frac{q}{kT} I_{D} τ

(2.3)

Note that this models a (very much) voltage dependent capacitance for the forward biased junction. This capacitance adds to (and can be dominant over) the depletion layer thickness related capacitance in section 2.3.2.

2.3.4 Modelling the diode

A sufficiently accurate model of the diode is now the combination of all previous voltage-current and voltage-capacitance relations for p-n junctions:

\begin{array}{rcl} i_{D} & = & I_{D 0} (e^{\frac{q \cdot v_{D}}{kT}} - 1) \end{array}

\begin{array}{rcl} I_{D 0} & = & A \cdot q \cdot (\frac{D_{p}}{L_{p}} \frac{1}{N_{D}} + \frac{D_{n}}{L_{n}} \frac{1}{N_{A}}) \cdot C \cdot {(kT)}^{3} e^{- \frac{W_{g}}{kT}} \\ C_{depl} & = & \frac{C_{0}}{{(1 - \frac{v_{D}}{φ_{0}})}^{m}} \\ C_{diff} & = & C_{0, diff} \cdot e^{\frac{q \cdot v_{D}}{kT}} \end{array}

About all “constants” in these relations depend on dopant levels, physical dimension, the material and the temperature. The diode symbol, with voltage and current convention and the i-v and C-v characteristics for some silicon diodes are shown in the figure below.

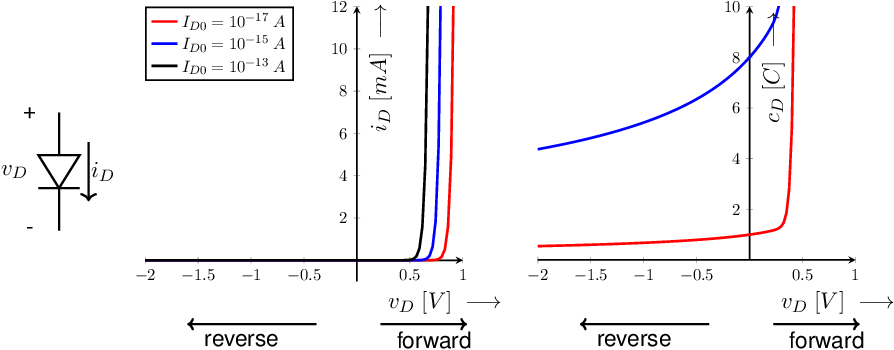
In the graph in the middle of Figure 2.6, current-voltage curves are shown for 3 different values of $I_{D 0}$ . These different $I_{D 0}$ correspond to (silicon) diodes with very different physical sizes. Note that — due to the exponential nature of the i-v-relation — all i-v curves have the same shape but appear to be shifted on the $v_{D}$ -axis.

The graph on the right hand side shows the diode capacitance as a function of $v_{D}$ . Again, the two curves correspond to (silicon) diodes with different sizes and dopant levels. These $C (v_{D})$ -curves are relatively flat in reverse, i.e. for $v_{D} < 0$ and are quite steep in forward.

2.3.5 Modelling the diode - simplified

On a linear-linear plot, the exponential $i_{D} - v_{D}$ relations appear to (nearly) zero, below some specific $v_{Dx}$ while the i-v curve seems to rise rapidly above that $v_{Dx}$ . This can be observed in e.g. Figure 2.6. where that $v_{Dx}$ is somewhere between 0.6 and 0.8 V. Zooming in on (or out) an exponential curve yields the exact same curve, only shifted left (or right)¹⁷ . Therefore, the voltage at which the $i_{D} - v_{D}$ -curves appear to increase sharply in Figure 2.6 may seem quite arbitrary.

However, the performance of silicon diodes in forward is quite good if the forward voltage is between about 0.6V and 0.7V. The ins and outs of this are outside the scope of this book¹⁸ .

Operating a silicon diode between 0.6 V and 0.7 V results in a diode current range of almost a factor 100; the other way around: $v_{D}$ can be kept in the range between 0.6-0.7 V for a large range of $i_{D}$ . Noting that for that large $i_{D}$ -range the $v_{D}$ does not change significantly, a silicon diode in forward may be modelled as a DC voltage source having a voltage of about 0.6... 0.7 V.

Having a significant current at $v_{D} \approx 0.6 . . . 0.7 V$ results in having a much lower current below $v_{D} \approx 0.6 V$ . A frequently sufficiently accurate model for a silicon diode is that the diode current is (near) zero for $v_{D} < 0.6 V$ . This behavior can be modelled as an open.

Combining these crude simplifications lead to a model for a (silicon) diode that is sufficiently accurate for many situations: behaving (almost) as an open for $v_{D}$ lower than about $0.6 . . . 0.7$ V and behaving (almost) as a voltage source for positive diode currents $i_{D}$ :

2.4 Bipolar junction transistors (BJTs)

A Bipolar Junction Transistor (BJT) is a smart extension of a diode. In a diode, holes move from p to n and electrons flow from n to p, where for both current components the $v - i$ -relation is exponential:

\begin{array}{rcl} i_{p} & = & I_{P 0} \cdot (e^{\frac{q \cdot v_{D}}{kT}} - 1) \\ i_{n} & = & I_{N 0} \cdot (e^{\frac{q \cdot v_{D}}{kT}} - 1) \\ i_{D} & = & i_{p} + i_{n} = I_{D 0} \cdot (e^{\frac{q \cdot v_{D}}{kT}} - 1) \end{array}

In a diode, both current components flow through the diode and through the same terminals. They must, since there is no other place to go in a device with only two terminals... However, in a BJT one of these two current components is redirected to a new — third — terminal that collects this redirected current component. Unfortunately, the other current component is still present and this current component represents an unwanted — drive — current.

There are 2 types of BJTs:

one type has a wanted current component consisting of electrons that flow from an N-type region through a P-type region to another N-type region. This type of BJT is called NPN-transistor after its internal structure.
the other type has a wanted current component of holes that flow from a P-region, via an N-region to another P-region. This is called a PNP-transistor.

The behavior of these two types of bipolar transistors is the exactly the same, except for the type of charge carrier. This difference results in a change of current direction and a change of polarity of the voltage on the terminals. Usually the NPN transistor is easier to understand than the PNP transistor: there are less minus signs involved in its element equations. That’s the main difference, really.

A schematic view of the principle of the operation of BJTs is shown in Figure 2.8. Right next to the cross sections of the NPN and PNP are the schematic symbols for these transistors. The emitter is identified by the arrow; the direction of the arrow is in the direction of the current flow in [A]. The collector is the opposite terminal and the base terminal is in the middle. The symbol itself resembles the physical construction of the very first bipolar transistor as constructed at Bell Labs in the late 1940s.

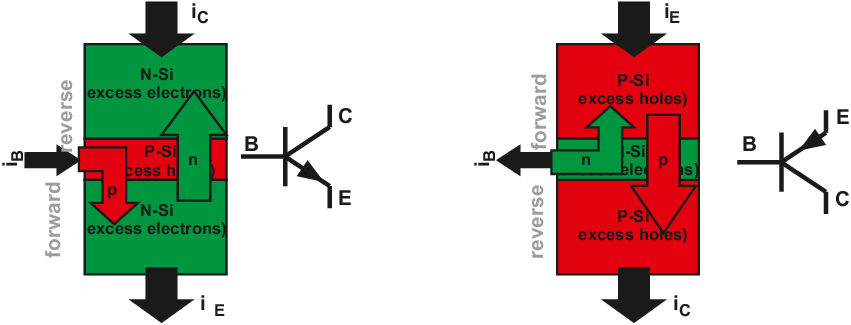
In order to get significant currents, one of the junctions must be in forward. That way, both a large electron and hole current component result. Only one of these components will be directed to the third terminal to create the output current. To ‘catch’ this wanted component the other junction must be in reverse (or at least far less in forward). Naming the parts:

The region from which the charge carriers that form the wanted current component originate is called the emitter, which is based on the Latin word for “send out”. The symbol used for this node is E.
The region where this wanted current component flows into is called the collector, based on the Latin word to gather up. The collector is usually identified by a C.
The middle region is called base, for historic reasons.
The current component that goes all the way through the device is the wanted current $i_{C}$ , which can be influenced exponentially with the voltage across the forward junction $v_{BE}$ . If you do everything right, this current is (almost) independent of the voltage across the other junction $v_{CB}$ and thus is also largely independent of $v_{CE}$ .
The other current component (the unwanted current that doesn’t flow through the entire device, $i_{B}$ ) is proportional to $i_{C}$ . If the device is properly designed the proportionality factor $β_{fe} = \frac{i_{C}}{i_{B}}$ can easily be around 100.

Summarized in equations, the behavior of a BJT resembles that of a diode. If the BC-junction is in reverse — which is the case in the normal operating range — we have for an NPN transistor the following element equations..

\begin{array}{rcl} i_{C} ≅ I_{C 0} (e^{\frac{q \cdot v_{BE}}{kT}} - 1) \\ i_{B} ≅ \frac{i_{C}}{β_{fe}} & (2.4) \\ i_{E} ≅ \frac{β_{fe} + 1}{β_{fe}} i_{C} \end{array}

For its PNP-equivalent the currents and voltages are inverted, but the equations are (up to minus signs) the same.

Similar to the situation for the diode, $I_{C 0}$ depends on the semiconductor material, dopant levels, sizes, and is very temperature dependent. The assumption that the BC-junction is in reverse is actually not necessary: the actual requirement for proper operation of a BJT is that the BE-junction is much more in forward than the BC-junction. Noting that the current-voltage relation of a junction is exponential it is sufficient to satisfy (for an NPN)

e^{\frac{q \cdot v_{BE}}{kT}} > > e^{\frac{q \cdot v_{BC}}{kT}}

and assuming that a current ratio of 100 satisfies this “much bigger” we get (again for an NPN)

e^{\frac{q \cdot v_{BE}}{kT}} > 100 \cdot e^{\frac{q \cdot v_{BC}}{kT}} \Leftrightarrow (v_{BE} - v_{BC}) > \frac{kT}{q} \ln (100) ≅ 120 mV \approx 100 mV

For the PNP-equivalent you should include a ”-”-sign for the voltages. If the $v_{CE}$ is smaller than about 100mV, an explicit $v_{CE}$ -dependency must be included:

i_{C} ≅ I_{C 0} (e^{\frac{q \cdot v_{BE}}{kT}} - 1) \cdot (1 - e^{\frac{- q v_{CE}}{kT}})

(2.5)

The operating range in which the second term on the right hand side in (2.5) is significant, is called saturation and hence is for $v_{CE} < 100 mV$ . In saturation, the collector current $i_{C}$ changes strongly with $v_{CE}$ .

Figure 2.9 shows the collector and base currents of a BJT as a function of $v_{BE}$ and $v_{CE}$ , on linear axes. For the curves, a typical $β_{fe} = 100$ was used, resulting in a hardly visible $i_{B} - v_{BE}$ curve. In the $i_{C} - v_{CE}$ plot 3 curves are shown, for $v_{BE}$ values each 18mV different. Due to the exponential $i_{C} - v_{BE}$ dependency, each 18mV difference in $v_{BE}$ results in a factor 2 difference in $i_{C}$ at room temperature.

2.4.1 Temperature dependency of the BJT currents

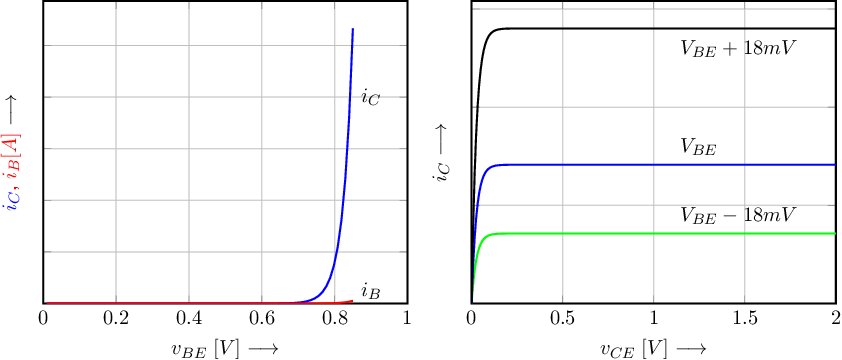
The voltage-current relation of the BJT is quite similar to that of a diode. The impact of temperature is also pretty much the same. Hence, the collector current (at constant $v_{BE}$ ) increases about exponentially with temperature around room temperature, showing a doubling for every 10K increase in temperature. At fixed collector current, the $v_{BE}$ decreases about 18mV for every 10K increase in temperature.

2.4.2 BJT $i_{C}$ - $v_{CE}$ -dependencies

The ideal(ized) element equations for the bipolar junction transistor are listed below. In this section we ignore any dependency in the pre factor $I_{C 0}$ for simplicity reasons. Assuming that the BC-junction is sufficiently in reverse, idealized, from (2.4),

\begin{array}{rcl} i_{C} ≅ I_{C 0} (e^{\frac{q \cdot v_{BE}}{kT}} - 1) \\ i_{B} ≅ \frac{i_{C}}{β_{fe}} & (2.6) \\ i_{E} ≅ \frac{β_{fe} + 1}{β_{fe}} i_{C} \end{array}

Without the explicit assumption of having the BC-junction in reverse, the collector current-voltage relation is, from (2.5),

i_{C} ≅ I_{C 0} (e^{\frac{q \cdot v_{BE}}{kT}} - 1) \cdot (1 - e^{\frac{- q v_{CE}}{kT}})

(2.7)

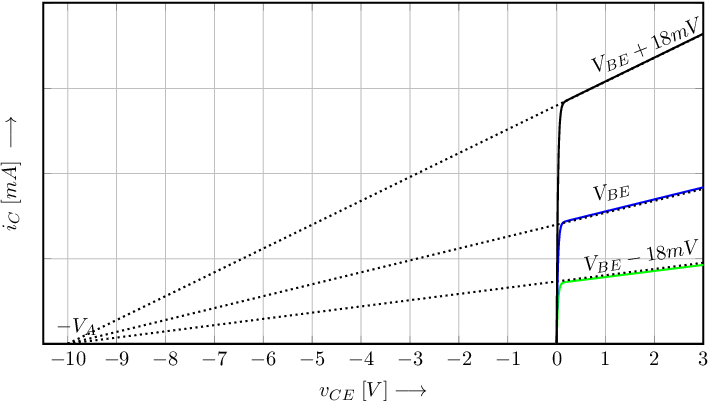
The last term on the right hand side in this relation is significant for roughly $V_{CE} < 100 mV$ . Also in this voltage range the current gain shows a significant voltage dependency. Another voltage dependency of the collector current is that the collector current $i_{C}$ increases with higher $V_{CE}$ voltages, due to the so-called base width modulation. With base width modulation, the thickness of the depletion layer associated with the BC-junction increases with increasing $V_{BC}$ and thereby modulates the effective (not depleted) width of the base region. The figure below shows the impact of this base width modulation on the collector current $i_{C}$ . It appears that extrapolated $i_{C} - v_{CE}$ -curves cross the $v_{CE}$ axis in about the same $v_{CE}$ , leading to

i_{C} ≅ I_{C 0} (e^{\frac{q \cdot v_{BE}}{kT}} - 1) (1 + \frac{v_{CE}}{V_{A}})

(2.8)

In this relation $V_{A}$ is a transistor-dependent constant, usually denoted as the Early voltage, named after one of the early guys modelling this effect.

2.4.3 Capacitive effects in BJTs

A bipolar junction transistor consists of two junctions that both have capacitive effects similar to those described for individual junctions. The junction between base and emitter is in forward in normal operation of the transistor, while the collector-base junction typically is in reverse. Their voltage dependent capacitive behavior is very similar to that described in §2.3.2 respectively in §2.3.3.

2.4.4 Current gain naming conventions

In literature, there are multiple ways to define the current gain of a BJT and there are even multiple names for each of these ways. The two usual ways to define the current gain are:

\begin{array}{rcl} current gai n_{fe} & = \frac{i_{C}}{i_{B}} \\ current gai n_{fb} & = \frac{i_{C}}{i_{E}} \end{array}

where the “f” in the subscript denotes regular forward operation of the BJT. The second letter in the subscript denotes the reference node. Hence, with the “fe” subscript, forward operation is assumed having the emitter as reference node and hence having as “free” terminals the base and the collector nodes. The symbols that are typically used for this are $α_{fe}$ , $β_{fe}$ and $h_{fe}$ . In this book, $β_{fe} \equiv \frac{i_{C}}{i_{B}}$ is used. Typically $i_{C} > > i_{B}$ and consequently $β_{fe} > > 1$ , usually $β_{fe} \approx 100$ for discrete BJTs.

Using the base as reference node, the current gain is $\frac{i_{C}}{i_{E}}$ and the symbols used then are $α_{fb}$ , $β_{fb}$ and $h_{fb}$ . In this book, this way of describing the current gain of a bipolar transistor is NOT used. Note that $α_{fb} = β_{fb} \equiv \frac{β_{fe}}{β_{fe} + 1}$ and hence with a large $β_{fe}$ , the $α_{fb}$ is a little smaller than 1.

2.5 MOS-transistors

A MOS-transistor is basically an adjustable resistor. Conduction takes place between two terminals: the region from where the charge carriers start to flow is called ‘source’, whereas the drain is called ‘drain’¹⁹ . The degree of conduction is determined (among others) by the gate-source voltage. In this book, the body node is (implicitly assumed to be tied to the source for simplicity reasons. In advanced electronics courses and design, this simplification is frequently not made.

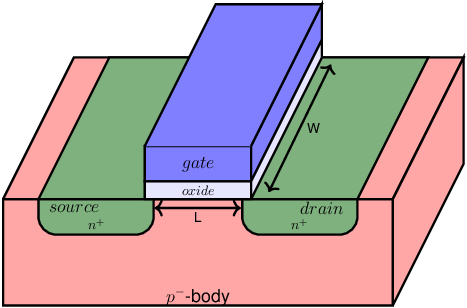
To briefly explain the operation of a MOS transistor, an N-type device is assumed in which electrical current is due to moving electrons from source to drain. Similar to the BJT, there is also a P-type device that operates identically although with holes instead of with electrons which results in opposite current directions and reversed voltage polarities compared to those in the N-device. For simplicity reasons, in this course the middle region — the $p^{-}$ bulk for the N-type MOS transistor — is assumed to be electrically connected to the source region.

The cross section shows the (slightly P-doped) substrate containing a heavily N-doped source region and a heavily N-doped drain region. The controlling element is the gate, which is very low ohmic²⁰ and is insulated from the substrate by a non-conducting layer of oxide. This yields a Metallic-Oxide-Semiconductor-structure.

The naming convention for the source region and drain region is based on the direction of the flow of the charge carriers: charge carriers by definition move from the source to the drain. For N-type transistors this means that the source potential is always lower than or equal to the drain potential.

The effect of the gate

For a qualitative explanation of the operation of a MOS-transistor, we need four basic principles:

Electrons flow from a lower potential to a higher potential;
Holes flow from a higher potential to a lower potential;
A voltage drop across a structure yields an electric field;
$n \cdot p = n_{i}^{2}$ , where $n$ and $p$ are the density of electrons and the density of holes respectively, and $n_{i}$ is the density of electrons that “evaporate” from the valence band into the conduction band for your semiconductor material. This relation is due to semiconductor physics and will not be motivated or discussed in depth in this book.

Now, we will first investigate a part of the MOS-transistor: we leave the source and drain out for the moment. This is shown in the figure below, and is what is called the MOS-capacitor²¹ .

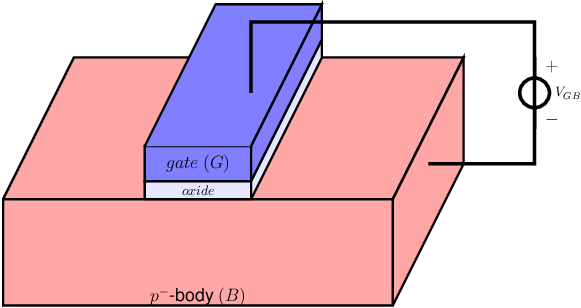
We can now distinguish three cases²² :

no voltage difference between the terminals: $V_{GB} = 0$
the potential at the gate is higher than the one at the substrate (body)): $V_{GB} > 0$
the potential at the gate is lower than the one at the substrate (body): $V_{GB} < 0$

For a zero voltage drop, $V_{GB} = 0$ , the electric field inside the oxide is zero. According to Poisson’s Law this means that there is no charge build-up in neither gate nor substrate. If you don’t know or don’t like Poisson’s equation, please think of the structure as a plate capacitor: with zero voltage across the plates the charge storage is zero. It is very much related with the element equation of a capacitor $Q = C \cdot V$ .

For $V_{GB} < 0$ there is a non-zero electric field in the oxide layer. Due to this electrical field holes are attracted to the semiconductor-oxide interface while electrons are pushed away from it: due to the $V_{GB} < 0$ the concentration of holes is increased near the oxide layer, while the electron concentration is decreased (compared to the case where $V_{GB} = 0$ ).

For $V_{GB} > 0$ , also a non-zero electric field will be present, but the polarity has changed. This causes the electrons to be attracted towards the oxide, while holes are repelled. As a result, the electron concentration has increased near the oxide-substrate interface, and the concentration of holes is decreased (compared to the case where $V_{GB} = 0$ ).

Weak inversion, depletion, strong inversion

In the discussion above, the last case is most interesting: $V_{GB} > 0$ . In this case, mobile holes are repelled from the oxide-substrate interface and electrons are attracted to it. We can distinguish three levels or attraction:

For small $V_{GB} > 0$ , a small amount of holes are pushed away: the P-type material becomes a little “less P”. What remains is called the depletion layer in which there are less mobile charge carriers (electrons or holes) than in the material under zero electric field. One should note that the concentration of electrons has risen simultaneously, since $n \cdot p = n_{i}^{2}$ .
When $V_{GB} > 0$ increases, more holes are being pushed away and simultaneously more electrons are attracted towards the oxide-substrate interface. If the concentration of electrons exceeds the concentration of holes, the semiconductor material is said to be in inversion. If, furthermore, both hole and electron concentrations are below doping level concentration of the semiconductor material, this region of operation is called weak inversion.
If an even larger $V_{GB} > 0$ is applied, even more holes are being pushed away and the concentration of electrons rises even further. When the electron concentration at the interface exceeds the P-type doping level of the semiconductor material this region of biasing is called strong inversion.

The current through a MOS transistor in weak inversion is determined by diffusion of carriers, similar to the mechanism in a diode or in a BJT. As a result, the $v - i$ -characteristic of a MOS transistor in weak-inversion greatly resembles that of a BJT. In this book, the weak inversion operation mode is not taken into account: the current in this region is relatively low and consequently throughout the book weak-inversion current is modelled as zero, zip, nil.

2.5.1 MOS-transistor in strong inversion

In inversion, the excess charge carriers that were originally in the bulk semiconductor material are being pushed away from the oxide-substrate interface and the opposite charge carriers are attracted to the interface. As explained before, for an N-type MOS transistor the bulk is $p^{-}$ material and the original (majority) carriers are holes. For P-channel transistors it is the complementary situation.

If in a MOS transistor the electrical fields (and hence the applied voltages) are such that the carrier concentration at the semiconductor-oxide interface equals that of the situation without any field but having the opposite type of carriers (e.g. electrons in the P-type bulk of an N-type MOS transistor), the transistor is in inversion. The applied $v_{GB}$ for this situation is usually denoted as the threshold voltage $V_{T}$ of the MOS transistor. For higher fields (absolute values of applied voltages) the MOS transistor is in strong inversion; there the concentration of electrons that are sucked to the interface exceeds the original hole concentration of the semiconductor material.

In strong inversion the current mechanism is dominated by drift, similar to the mechanism in plain resistors. Therefore, the MOS transistor in strong inversion is similar to an adjustable — but non-linear — resistor: there are two $n +$ terminals (source and drain) connected by a now N-type region, in which the concentration of mobile electrons can be varied by adjusting $v_{GB}$ . For low $v_{DS}$ , the situation is depicted in the following figure:

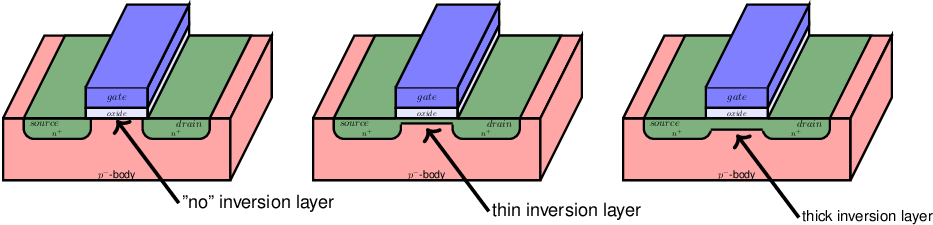
If there is no inversion layer present, the conduction between source and drain is zero²³ . If there is an inversion layer present, we effectively created a resistor, where the resistive value depends on the thickness of the inversion layer:

$n^{+}$ - n - $n^{+}$ in a thin inversion layer; for small $v_{GS}$ ( $= v_{GB}$ )

$n^{+}$ - n - $n^{+}$ in a somewhat thicker layer; for somewhat higher $v_{GS}$

$n^{+}$ - n- $n^{+}$ in a thick inversion layer; for high $v_{GS}$

The electrical conductivity of a material is proportional to the product of mobile charge carriers and their mobility. From this it becomes clear that by varying the electron concentration between source and drain, we can alter the conductivity between source and drain. Of course it is possible to derive a mathematical expression for this relation, but we will not do it. We will however give the resulting element equations in the next section.

2.5.2 MOS-transistor in strong inversion: ideal case summary

For the N-type MOS transistor to be in strong inversion:

v_{GS} > V_{T}

(2.9)

The region where there is an appreciable effect of $V_{DS}$ on the drain current is denoted the “linear” or “triode” region. These names originate from the quite linear dependence of the drain current on both $V_{DS}$ and $V_{GS}$ for low $V_{DS}$ values, and its close resemblance with the electrical behavior of a triode vacuum tube. In most circuits analyzed and designed throughout this book, this region is avoided. The set of element equations of an NMOS transistor in this region is:

\begin{array}{rcl} i_{D} = K ((v_{GS} - V_{T}) v_{DS} - \frac{v_{DS}^{2}}{2}) & (2.10) \\ i_{G} = 0 \\ v_{DS} \leq v_{GS} - V_{T} \\ v_{GS} > V_{T} \\ K = \frac{W}{L} \cdot μ C_{□} (material and geometry and size dependent) \\ i_{D} = 0 for v_{GS} < V_{T} \end{array}

The element equations for its PMOS-equivalent are basically the same, except for many ”-”-signs, due to the fact that conduction in PMOS-transistors is using holes whereas in NMOS-transistors it is using electrons.

The current factor $K$ in the element equation depends on some technology parameters — the carrier mobility $μ$ and the oxide capacitance per square unit area $C_{□}$ — and the width (out-of-the-page) and length (distance between source and drain) of the MOS transistor. In this book, we will assume $K$ to be a known and fixed constant for transistors although they may be different for different transistors as these may have different width $W$ and length $L$ and may be build in a different semiconductor material which impacts the carrier mobility $μ$ . The threshold voltage $V_{T}$ is also determined by the technology — mainly by the doping levels and the oxide thicknesses — and will also be assumed constant and known.

For $v_{DS} > v_{GS} - V_{T}$ , the relations in (2.10) do not hold anymore. The element equations for the region where $v_{DS} > v_{GS} - V_{T}$ can be obtained from the ones in (2.10) by substituting $v_{DS} = v_{GS} - V_{T}$ . Then the $i_{D}$ is almost independent of $v_{DS}$ , with a square law dependence between $i_{D}$ and $v_{DS}$ ; this region is denoted as saturation²⁴ while the element equation is called the square law relation:

\begin{array}{rcl} i_{D} = \frac{1}{2} \cdot K \cdot {(v_{GS} - V_{T})}^{2} & (2.11) \\ i_{G} = 0 \\ v_{DS} \geq v_{GS} - V_{T} \\ v_{GS} > V_{T} \\ K = \frac{W}{L} \cdot μ C_{□} \\ i_{D} = 0 for v_{GS} < V_{T} \end{array}

Figure 2.14 shows (left graph) the drain current $i_{D}$ as a function of the gate-source voltage $v_{GS}$ for a few values of $v_{DS}$ and (right) $i_{D}$ as a function of the drain-source voltage $v_{DS}$ for a few values of $v_{GS}$ . These curves are for an N-type MOS transistor having a threshold voltage $V_{T} = 1 V$ . Note in both plots in Figure 2.14 the transition between the linear region and the square law region, at $v_{DS} = v_{GS} - V_{T}$ .

2.5.3 MOS-transistor symbols

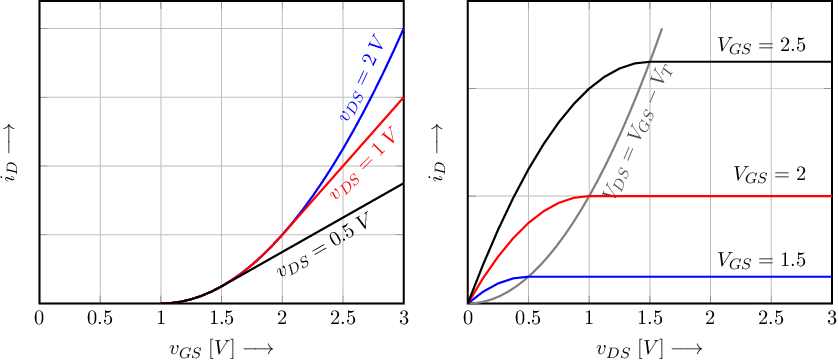
Figure 2.15 shows both the cross section and the circuit schematic symbols for NMOS transistors and PMOS transistors. These two are — similar to NPNs and PNPs — basically each other’s complement: they operate on the opposite type of charge carriers and hence have opposite voltages and current directions. Identical to the situation for BJTs, the source node is marked by the arrow whereas the direction of that arrow is in the direction of the current in [A].

2.5.4 MOS transistor output resistance

The output resistance of an MOS transistor in the linear region, for which (2.10) hold, follows directly from the definition of resistance:

\begin{aligned} r_{out} & = {(\frac{\partial i_{D}}{\partial v_{DS}})}^{- 1} \\ = \frac{1}{K (v_{GS} - V_{T} - v_{DS})} for v_{GS} > V_{T} + v_{DS} \end{aligned}

(2.12)

According to the simplified relation in (2.11) the MOS transistor exhibits infinite output resistance in its square law region. However, similar to the case for the BJT, an actual MOS transistor has a non-zero dependency of $i_{D}$ on $v_{DS}$ in the square law region. For MOS transistors this effect is due to an effect similar to the bipolar base width modulation, now called channel length modulation. On top of that there are other effects, including drain-induced barrier lowering, hot carrier effects and more. Here we will not dig into these, but only model these combined effects by again an Early voltage $V_{A}$ or a channel length modulation parameter $λ$ :

\begin{aligned} i_{D} & ≅ \frac{1}{2} K {(v_{GS} - V_{T})}^{2} (1 + \frac{v_{DS}}{V_{A}}) \\ = \frac{1}{2} K {(v_{GS} - V_{T})}^{2} (1 + λ \cdot v_{DS}) \end{aligned}

leading to

\begin{array}{rcl} r_{out} & = {(\frac{\partial i_{D}}{\partial v_{DS}})}^{- 1} \\ = \frac{V_{A}}{\frac{1}{2} K {(v_{GS} - V_{T})}^{2}} ≅ \frac{V_{A}}{I_{D}} \\ ≅ \frac{1}{λ \cdot I_{D}} & (2.13) \end{array}

2.5.5 MOS transistor “on-state” and “off-state” resistance

In this reader, MOS transistors are typically used in circuits as (power) amplifying components. These are used throughout this book mainly in linear (analog) applications such as amplifiers, amplifier stages and harmonic oscillators. This is covered in many of the next chapters.

However, MOS transistors are also very well suited for e.g. low power switching applications, in digital gates such as NAND gates, NOR gates, pass gates, inverters and much more. Also explicit usage as high power switches in for example switched mode power amplifiers and switched mode supplies, converters and inverters are well known applications for transistors.

For switching applications, usually MOS transistors are used to implement the “switch”; the MOS transistor is the switched between maximally on and completely off. From (2.10) or (2.11) the “completely off” case is satisfied for $v_{GS} < V_{T}$ . Typically typically $V_{T} > 0$ and then the completely off state can be accomplished by setting $v_{GS} = 0$ and the (ideal) “off-state” current is $0 A$ and the “off-state” resistance is

\begin{array}{rcl} r_{off} \to \infty for v_{GS} < V_{T} \end{array}

The “on-state” resistance in switching applications is typically low enough to ensure that the MOS transistor operates in its linear region, satisfying (2.10). Then the “on-state” resistance is given by (2.12). Assuming that the MOS transistor is a good switch, $v_{DS} < < v_{GS} - V_{T}$ which leads to the following approximation for on-resistance:

\begin{array}{rcl} r_{on} & \approx \frac{1}{K (v_{GS, on} - V_{T})} for v_{GS} > > V_{T} + v_{DS} \end{array}

2.5.6 MOS transistor input capacitance, input current and input power

In the simplified equations (2.10) and (2.11) the input current is modelled as 0. At low frequencies this is a decent approximation. At high frequencies and at steep switching edges this is however not a proper model. Being a charge controlled device, see section 2.5.1, the inversion layer that takes care of conduction between source and drain is formed by some sort of capacitance between gate and inversion layer. It can be derived that the charge required to change the $v_{GS}$ is very similar to that required for an ordinary plate capacitance. Assuming that there is no inversion layer for $v_{GS} < V_{T}$ , the gate charge $Q_{G}$ in various regions of operation is

\begin{array}{rcl} Q_{G} & \approx 0 for v_{GS} < V_{T} \\ Q_{G} & \approx C_{gate} \cdot (v_{GS} - V_{T}) for v_{GS} > v_{DS} + V_{T} (linear region) \\ Q_{G} & \approx \frac{2}{3} C_{gate} \cdot (v_{GS} - V_{T}) for v_{GS} > V_{T} v_{DS} > v_{GS} - V_{T} (square law, saturation) \end{array}

An idealized model for the gate current $i_{G}$ of a MOS transistor is then

\begin{array}{rcl} i_{G} = \frac{\partial Q_{G}}{∂t} & ≅ 0 (in the off state) \\ ≅ C_{gate} \cdot \frac{\partial v_{GS}}{∂t} (linear region) \\ ≅ \frac{2}{3} \cdot C_{gate} \cdot \frac{\partial v_{GS}}{∂t} (square law region) \end{array}

At very high frequencies this drive current can be significant, especially for high power transistors for which the physical size and hence its $C_{gate}$ are large.

Driving a transistor in strong inversion, saturation from a sinusoidal source or from a driving circuit that provides $v_{GS} = V_{gs} \sin (ωt)$ , the gate current is $i_{G} \approx ω V_{gs} C_{gate} \cos (ωt)$ which obviously corresponds to the situation of driving a capacitor $C_{gate}$ . Note that at high frequencies and high signal amplitudes this input current can be large. Using a MOS transistor as switch, $Q_{G}$ must be sourced or removed within the duration of a rising or falling edge of the driving signal. Assuming for example a switching frequency $f_{switch}$ and edges that are 10% of the switching period, $i_{G} \approx Q_{G} \cdot 10 \cdot f_{switch}$ where $Q_{G}$ is given a few equations back. At high switching frequencies this input current can be quite high.

Driving the MOS transistor from a (resistive) source, the power required to drive the transistor can be derived to be

\begin{array}{rcl} P_{G} & = f_{switch} \cdot Q_{G, on} \cdot V_{gs, on} \\ \approx f_{switch} \cdot C_{gate} \cdot V_{gs, on}^{2} \end{array}

[prev] [prev-tail] [front] [up]