Amplifier circuits

5 Amplifier circuits

5.1 Basic amplifier circuits

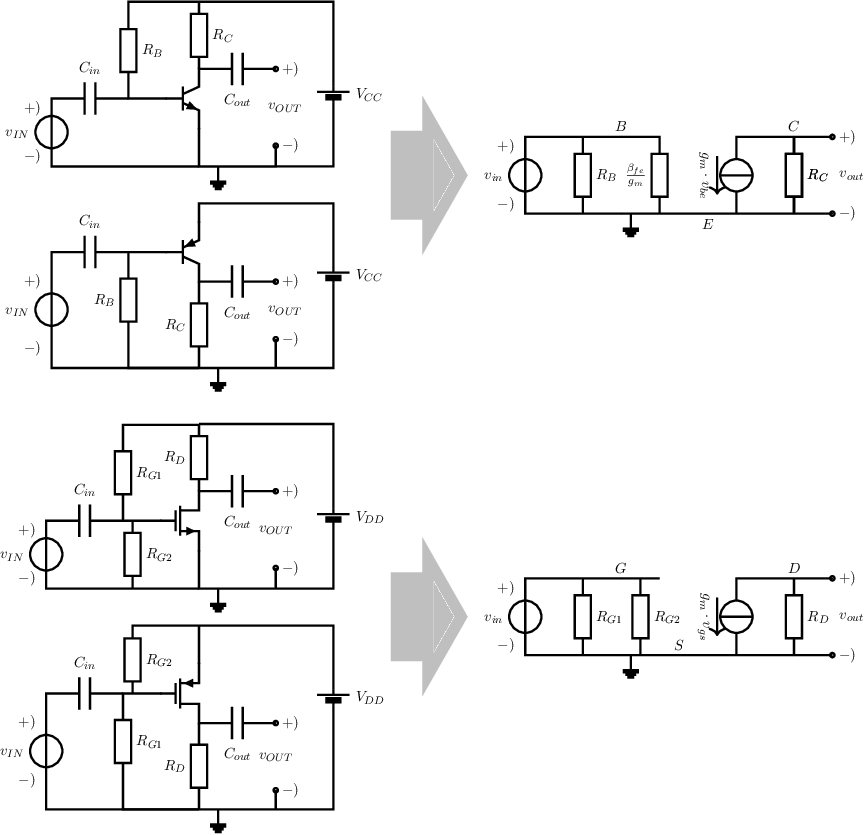
In chapter 4, two simple amplifier circuits were analyzed using small signal equivalent circuits. Figure 4.13 showed a very basic amplifier with one BJT (and its SSEC). In that circuit, the transistor is driven at the $B - E$ port while the output port is between $C$ and $E$ . This may be somewhat hard to see in the original circuit, but for sure it is very visible in its SSEC. The MOS version is shown in Figure 4.16, in which the transistor is driven at the $G - S$ port and where the output port includes the $D$ and the $S$ terminals. These circuits are both repeated in Figure 5.1 along with their P-type equivalents.

pict — Figure 5.1: Amplifier circuits with BJT and MOST from chapter 4, with their SSEC

In general a transistor is a three terminal device that behaves like a (nonlinear) voltage controlled current source (VCCS). To be able to behave like a VCCS a device must be at least a two-port device. From a fundamental point of view a two-port device has 4 terminals, whereas a transistor has just 3 which implies that the two ports share one terminal.

For a circuit using a BJT this yields 3 ways to share terminals between input and output port:

a common-emitter circuit (CEC) in which the emitter is shared by the input port and output port. Due to the nature of the BJT, the input port must be formed by the $v_{be}$ voltage while the output port voltage is $v_{ce}$ . The emitter node is common in the input and output port, hence the name CEC.
a common-base circuit (CBC) in which the base is shared by the input port and output port. So the input port must be formed by the $v_{be}$ voltage while the output port voltage is $v_{cb}$ .
a common-collector circuit (CCC) in which the collector is shared by the input port and output port. Therefore for this case, the input port must be formed by $v_{bc}$ while the output port voltage is $v_{ec}$ .

All these basic circuits using one BJT have distinct small-signal properties. The figure below lists the 3 possible configurations, starting from the generalized bias circuit for a BJT:

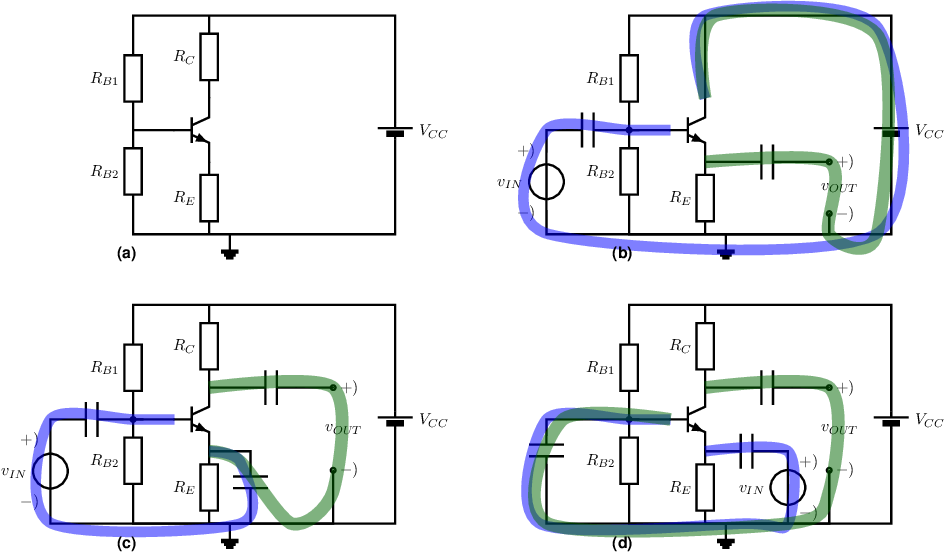
The generalized bias circuit for one BJT is shown in Figure 5.2a. In all circuits either the base or the emitter or both are directly driven by the input signal; driving is done via (DC blocking) capacitances. Drawing one voltage mesh including the input signal and one transistor node pair and drawing one voltage mesh that includes both the output port of the circuit and one transistor node pair directly reveals the common node (in both meshes). In this way Figure 5.2b represents the common-collector circuit (CCC), Figure 5.2c is the common-emitter circuit (CEC) and Figure 5.2d is the common base circuit (CBC).

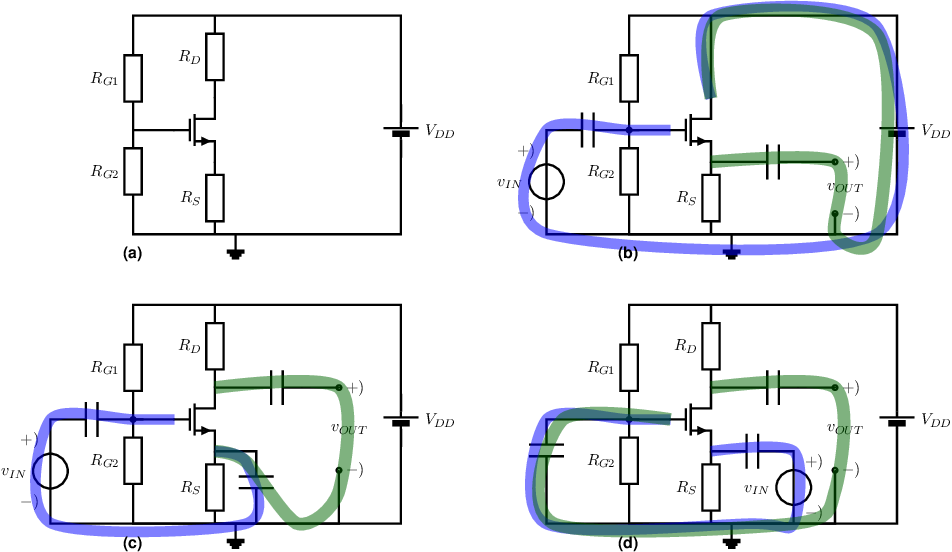
Equivalently, for basic amplifier circuits using a MOS transistor this yields:

a common-source circuit (CSC) in which the source is shared by the input port and output port. Due to the nature of the MOS transistor, the input port must be formed by the $v_{gs}$ voltage while the output port voltage is $v_{ds}$ .
a common-gate circuit (CGC) in which the gate is shared by the input port and output port. Hence the input port is formed by the $v_{gs}$ voltage while the output port voltage is $v_{dg}$ .
a common-drain circuit (CDC) in which the drain is shared by the input port and output port. Therefore the input port is formed by $v_{gd}$ while the output port voltage is $v_{ds}$ .

These three configurations are shown in figures 5.3c, d and b respectively.

5.1.1 The common-emitter circuit (CEC)

From the above description, it follows that the bipolar circuits in chapter 4 and the bipolar ones in Figure 5.1 are common-emitter circuits. As these CECs are analyzed in detail in §4.8 no analyses are given (or repeated) here.

5.1.2 The common-source circuit (CSC)

Similarly, the MOS circuits in chapter 4 and the MOS ones in Figure 5.1 are common-source amplifiers; analyses of its biasing and small signal properties are provided in §4.8.

5.1.3 The common-base circuit (CBC)

The CBC with an NPN is shown in Figure 5.4a; figure 5.4b gives its small-signal equivalent circuit for frequencies where the impedances $1 ∕ jω C_{1}$ , $1 ∕ jω C_{2}$ and $1 ∕ jω C_{3}$ are small enough to be negligible compared to the other impedances. This SSEC is now used to calculate some small-signal properties of the CBC: its input resistance $r_{in}$ and its output resistance $r_{out}$ , as well as the small signal voltage gain $H = v_{out} ∕ v_{in}$ .

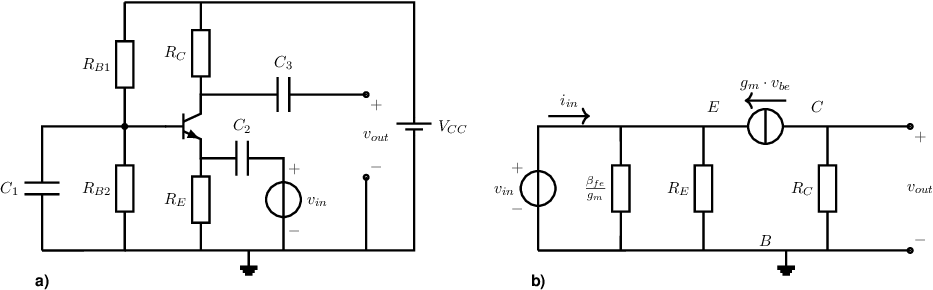
The small-signal input resistance is, by definition, the quotient of $v_{in}$ and $i_{in}$ . Using the brute force method, and using a driving voltage source:

\begin{array}{rcl} r_{in} = \frac{v_{in}}{i_{in}} \\ i_{in} = i_{re} - i_{b} - g_{m} \cdot v_{be} \\ i_{re} = \frac{v_{in}}{R_{E}} \\ i_{b} = \frac{g_{m} \cdot v_{be}}{β_{fe}} \\ v_{be} = - v_{in} \end{array}

Substituting these equations gives for the input resistance:³⁸

r_{in} = R_{E} ∕ ∕ \frac{β_{fe}}{g_{m}} ∕ ∕ \frac{1}{g_{m}}

(5.1)

Equation (5.1) shows that the input resistance of a CBC consists of three components. For decent BJTs, the current gain factor $β_{fe}$ is quite large, resulting in an $β_{fe} ∕ g_{m}$ term that is negligible compared to the $1 ∕ g_{m}$ term. Using the relation for transconductance of a BJT it follows that for the terms $R_{E}$ and $1 ∕ g_{m}$ :

\begin{array}{rcl} R_{E} & = \frac{V_{RE}}{I_{E}} and \frac{1}{g_{m}} = \frac{1}{\frac{q}{kT} \cdot I_{C}} ≅ \frac{\frac{kT}{q}}{I_{E}} \end{array}

from which we see both terms are identical in size for a DC bias voltage drop across $R_{E}$ as low as $kT ∕ q≅$ 25 mV. In pretty much all CBC circuits, this voltage drop across $R_{E}$ is significantly larger — usually at least some tenths of a volt — which gives an input resistance

r_{in} ≅ \frac{1}{g_{m}}

(5.2)

The small-signal voltage transfer is the ratio of voltage variation at the output due to a variation at the input. Again, using the brute force method:

\begin{array}{rcl} H = \frac{v_{out}}{v_{in}} \\ v_{out} = - i_{c} \cdot R_{c} \\ i_{c} = g_{m} \cdot v_{be} \\ v_{be} = - v_{in} \\ H & = \frac{v_{out}}{v_{in}} = g_{m} \cdot R_{C} & (5.3) \end{array}

Note that the input and output voltages are in phase, in contrast to the situation for the CEC where the gain is negative and hence the phase difference is (ideally) $18 0^{\circ}$ .

The small-signal output resistance of a circuit can be obtained in a number of ways. For linear circuits (as the SSEC), the three methods which are used most often are:

\begin{array}{rcl} r_{out} & = {\frac{{v_{out} |}_{r_{out} \to \infty}}{{i_{out} |}_{r_{out} = 0}} |}_{for equal v_{in}} \\ r_{out} & = {\frac{v_{out, forced}}{i_{out}} |}_{v_{in} = 0} \end{array}

or iin=0 rout = vout iout,forced | vin=0 or iin=0

Note that in the last two methods the input signal source is set to zero. For an input voltage source this translates in effectively shorting the input node in the SSEQ, while for an input current the input current source is to be replaced by an open. Application of the first method, using equation (5.3) gives:

\begin{array}{rcl} {v_{out} |}_{r_{out} \to \infty} = g_{m} \cdot R_{C} \cdot v_{in} \\ {i_{out} |}_{r_{out} = 0} = g_{m} \cdot v_{in} \\ r_{out} & = R_{C} \end{array}

This method requires 2 calculations, while the output of the amplifier at the other two methods is driven with a current or voltage source yielding the output impedance directly. These latter two methods are mostly used in this book.

For a CBC,

r_{in}

is low and

r_{out}

is high: the circuit acts like a “current-in-current-out” amplifier.

5.1.4 The common-gate circuit (CGC)

The MOS equivalent of the CBC is called a common-gate circuit, CGC; an implementation with an NMOS transistor shown in Figure 5.5. Its input resistance, voltage gain and output resistance will now be derived using Figure 5.5b:

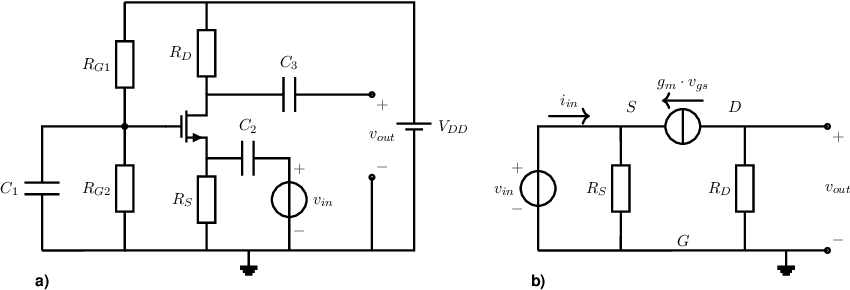
The small-signal input resistance of the circuit can be calculated using e.g. the brute force method. Driving the output with a voltage source and setting the input signal source to zero:

\begin{array}{rcl} r_{in} = \frac{v_{in}}{i_{in}} \\ i_{in} = i_{rs} - g_{m} \cdot v_{gs} \\ i_{rs} = \frac{v_{g}}{R_{S}} \\ v_{gs} = - v_{in} \\ r_{in} = R_{S} ∕ ∕ \frac{1}{g_{m}} ≅ \frac{1}{g_{m}} \end{array}

The small-signal voltage gain can be derived the same way as for the CBC: $H = v_{out} ∕ v_{in} = - g_{m} \cdot v_{gs} \cdot R_{D}$ while $v_{gs} = - v_{in}$ :

\frac{v_{out}}{v_{in}} = g_{m} \cdot R_{D}

(5.4)

The small-signal output resistance can readily be derived driving the output using e.g. a current source. Note that then all other independent sources are set to zero:

\begin{array}{rcl} r_{out} & = \frac{v_{out}}{i_{out}} \\ v_{out} = (i_{out} - i_{d}) \cdot R_{D} \\ i_{d} = g_{m} \cdot v_{gs} = 0 \\ r_{out} & = R_{D} \end{array}

5.1.5 The common-collector circuit (CCC)

The CEC and CBC — and their MOS equivalents CSC and CGC — are circuit configurations in which the transistor is driven between base and emitter for the BJT, and between gate and source for the MOS transistors. This nicely complies with the element equation for the two types of transistors where in the normal operating range of the transistors the output current is a function of the input voltage: $i_{C} (v_{BE})$ and $i_{D} (v_{GS})$ .

Another useful configuration is the common-collector circuit where the transistor is not directly driven between B and E or between G and S for MOS transistors. Instead, the transistor is driven at the base (gate) while the emitter (source) voltage is set via $i_{C}$ ( $i_{D}$ ) and serves as output voltage. The corresponding circuit schematic of the CCC with an NPN is given in Figure 5.6a.

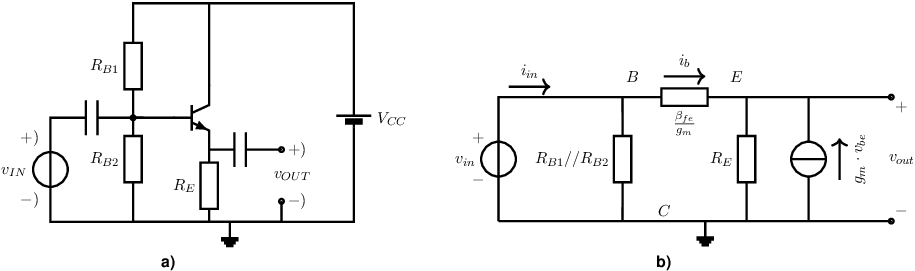
Feedback from output current to the non-driven input node is typically accomplished by a resistor (or impedance) $R_{E}$ . The highest attainable value for $R_{E}$ is $\infty Ω$ using a DC current source instead of $R_{E}$ .

Using a DC current source, it may be clear that the $v_{BE}$ of the transistor is fixed (assuming no external load and hence zero output currents). Then the difference between the input voltage of the CCC and its output voltage is merely a DC shift. The small-signal value of $v_{IN}$ equals that of $v_{OUT}$ and consequently in this case the small-signal gain is exactly one.

Figure 5.6b shows the small signal equivalent circuit, for frequencies where the impedances of the capacitances are negligibly small.

The input resistance Below, the input resistance of the CCC is derived using a driving voltage source. Note that — because of Ohm’s law — we would get a similar expression if we would have used a driving current source. We get:

\begin{array}{rcl} r_{in} = \frac{v_{in}}{i_{in}} \\ i_{in} = i_{RB 1 ∕ ∕ RB 2} + \frac{v_{be}}{β_{fe} ∕ g_{m}} \\ i_{RB 1 ∕ ∕ RB 2} = \frac{v_{in}}{R_{B 1} ∕ ∕ R_{B 2}} \\ v_{be} = v_{in} - R_{E} \cdot (g_{m} \cdot v_{be} + \frac{g_{m} \cdot v_{be}}{β_{fe}}) \end{array}

The equations above are sufficient to calculate everything within this circuit. Since the expression for $v_{be}$ depends on $v_{be}$ , we must separate the variables³⁹ , yielding:

\begin{array}{rcl} v_{be} = \frac{v_{in}}{1 + R_{E} \cdot g_{m} + R_{E} \cdot g_{m} ∕ β_{fe}} \\ i_{in} = \frac{v_{in}}{R_{B 1} ∕ ∕ R_{B 2}} + \frac{v_{in}}{β_{fe} ∕ g_{m} \cdot (1 + R_{E} \cdot g_{m} + R_{E} \cdot g_{m} ∕ β_{fe})} \\ r_{in} = {(\frac{1}{R_{B 1} ∕ ∕ R_{B 2}} + \frac{1}{β_{fe} ∕ g_{m} \cdot (1 + R_{E} \cdot g_{m} + R_{E} \cdot g_{m} ∕ β_{fe})})}^{- 1} \end{array}

After simplification of this relation, we may get (5.5). Note that simplification does not change the relation; it merely changes its form, appearance and its readability. The above derivation would have been shorter using a driving current source.

r_{in} = R_{B 1} ∕ ∕ R_{B 2} ∕ ∕ (\frac{β_{fe}}{g_{m}} + (1 + β_{fe}) R_{E})

(5.5)

It follows from this relation that the input resistance of the circuit is more or less equal to $β_{fe} \cdot R_{E}$ , parallel to the resistance of the input (bias) circuit: the input resistance of a CCC is usually relatively high.

The small signal voltage gain of the circuit equals the ratio between the small signal output voltage and the (driving) input voltage:

\begin{array}{rcl} H = \frac{v_{out}}{v_{in}} \\ v_{out} = R_{E} \cdot i_{e} \\ i_{e} = i_{b} + g_{m} \cdot v_{be} \\ i_{b} = \frac{v_{be}}{β_{fe} ∕ g_{m}} \\ v_{be} = v_{in} - v_{out} \end{array}

\begin{array}{rcl} i_{e} = \frac{v_{in} - v_{out}}{β_{fe} ∕ g_{m}} + g_{m} \cdot (v_{in} - v_{out}) \\ v_{out} = v_{in} \cdot R_{E} \cdot (\frac{g_{m}}{β_{fe}} + g_{m}) - v_{out} \cdot R_{E} \cdot (\frac{g_{m}}{β_{fe}} + g_{m}) \\ H = \frac{g_{m} \cdot R_{E} \cdot (\frac{1}{β_{fe}} + 1)}{1 + g_{m} \cdot R_{E} \cdot (\frac{1}{β_{fe}} + 1)} \end{array}

From the relation above, it follows that the small signal voltage gain is smaller than or equal to 1. The gain approaches 1 when either the transconductance $g_{m}$ or the resistance $R_{E}$ go to infinity. Note that if a current source would have been used instead of $R_{E}$ , the signal transfer (without load impedance) is exactly equal to 1. This circuit is commonly called an “emitter-ollower”⁴⁰ , since the output and input voltages have an equal phase and (almost) equal amplitude.

The output resistance In the derivation of the output resistance shown below, it is (arbitrarily) assumed that the output port is driven by a voltage source. In the derivation, all other independent sources must be set to zero (i.e. $v_{in} = 0$ ) yielding:

\begin{array}{rcl} r_{out} = \frac{v_{out}}{i_{out}} \\ i_{out} = - i_{b} + i_{RE} - g_{m} \cdot v_{be} \\ i_{b} = - \frac{v_{out}}{β_{fe} ∕ g_{m}} \\ i_{RE} = \frac{v_{out}}{R_{E}} \\ v_{be} = - v_{out} \\ i_{out} = v_{out} \cdot (\frac{g_{m}}{β_{fe}} + g_{m} + \frac{1}{R_{E}}) \\ r_{out} = R_{E} ∕ ∕ \frac{β_{fe}}{g_{m}} ∕ ∕ \frac{1}{g_{m}} & (5.6) \end{array}

The dominant factor in the expression for $r_{out}$ is the transconductance of the transistor $1 ∕ g_{m}$ . As numerical example, a bias current of 1 mA yields a small signal output resistance of less than 25 $Ω$ , which is quite low. Please keep in mind that this impedance is a small signal impedance: the output current $i_{out}$ should be (sufficiently) smaller than the bias current $I_{C}$ . In other words: although $r_{out}$ can be low, the circuit cannot provide significant output currents.

5.1.6 The common-drain circuit (CDC)

The MOS equivalent of the common collector circuit — the common drain circuit — is given in Figure 5.7a in an NMOS variant. The analysis of a CDC is analogous to that of the CCC and therefore only the resulting equations are given.

The input resistance From the small signal equivalent circuit in Figure 5.7b it is obvious that (for this simple SSEQ of a MOS transistor) the gate current is 0 A. The input resistance of the CDC is then equal to the parallel impedance of $R_{G 1}$ and $R_{G 2}$ which yields $r_{in} = R_{G 1} ∕ ∕ R_{G 2}$ .

The small signal signal transfer The voltage gain (or transfer) of input to output can be calculated in the same way as for the CCC, resulting in $\frac{v_{out}}{v_{in}} = \frac{g_{m} \cdot R_{S}}{1 + g_{m} \cdot R_{S}}$ which shows that the input signal and output signal are in phase. Analogous to the CCC, this circuit is called a “source-follower”.

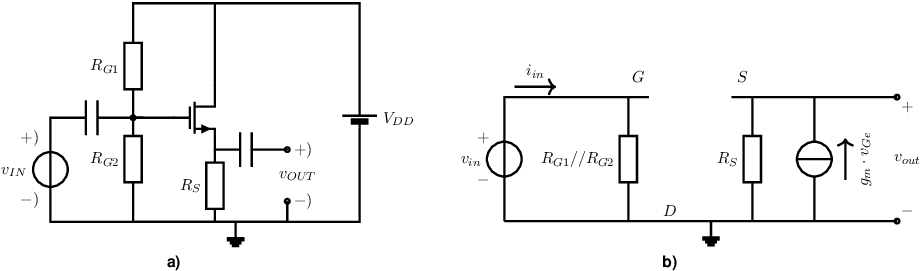
The output resistance can easily be obtained from the small-signal equivalent circuit by forcing e.g. a voltage at the output node for $v_{g}$ = 0:

r_{out} = R_{S} ∕ ∕ \frac{1}{g_{m}}

(5.7)

This small signal output resistance is typically dominated by the $1 ∕ g_{m}$ term. The small-signal $r_{out}$ can be low-ohmic (only) if the output current $i_{out}$ is sufficiently smaller than the bias current $I_{D}$ .

5.1.7 CEC, CBC, CCC, CSC, CGC and CDC: a comparison

All three variants of the single-BJT amplifier circuits have different small signal properties. Table 1 gives a comparative summary of the results of the three circuits with respect to signal transfer, input and output resistances.


circuit type	CEC	CBC	CCC

transconductance $g_{m}$ for given $I_{C}$	$(q ∕ kT) \cdot I_{C}$	$(q ∕ kT) \cdot I_{C}$	$(q ∕ kT) \cdot I_{C}$

input resistance	$≅ β_{fe} ∕ g_{m}$ (average)	$≅ 1 ∕ g_{m}$ (low)	$≅ β_{fe} \cdot R_{E}$ (high)

signal transfer or voltage gain	$≅ - g_{m} \cdot R_{C}$	$≅ g_{m} \cdot R_{C}$	$≅ 1$

output resistance	$≅ R_{C}$ (average)	$≅ R_{C}$ (average)	$≅ 1 ∕ g_{m}$ (low)

Table 1: Comparison of small signal properties for the CEC, CBC and CCC

An overview of a number of small signal properties for the three basic MOS circuits is given in Table 2.


circuit type	CSC	CGC	CDC

transconductance $g_{m}$ for $I_{D} = I_{C}$	$g_{mMOS} < g_{mBJT}$	$g_{mMOS} < g_{mBJT}$	$g_{mMOS} < g_{mBJT}$

input resistance	very high	$≅ 1 ∕ g_{m}$	very high

signal transfer or voltage gain	$≅ - g_{m} \cdot R_{D}$	$≅ g_{m} \cdot R_{D}$	$≅ 1$

output resistance	$≅ R_{D}$ (average)	$≅ R_{D}$ (average)	$≅ 1 ∕ g_{m}$ (low)

Table 2: Comparison of small signal properties for the CSC, CGC and CDC

5.2 More complex amplifiers

The basic circuits discussed in section 5.1 contain just one transistor. For some applications one of these circuits may do: if the set of small signal properties listed in Table 1 or in Table 2 satisfies all your requirements, you’re done.

However, many times none of the basic circuits in section 5.1 can satisfy a set of small signal requirements for a specific application. For example for an audio power amplifier a requirement may be to design a high $r_{in}$ , a low $r_{out}$ and a high voltage gain $| a_{v} |$ . None of the basic circuits in section 5.1 can achieve all these. The basic circuits can however partially satisfy the requirements, see Table 1 and Table 2. The fact that the basic circuits can in general not satisfy an arbitrary set of requirements is a direct consequence of the limited number of degrees of freedom in circuits with just one transistor. If we must satisfy multiple requirements — that are not compatible with any of the basic amplifier circuit — clearly more degrees of freedom must be created. In this chapter this is accomplished by mix-and-match of basic amplifiers into a larger amplifier. In chapter 8 this is extended to opamp-style circuits. As stated, in this section it is mix-and-match.

5.2.1 Mix-and-match

If a specific set of specifications must be met by a circuit — hereby an amplifier — that can only partially be met by any of the basic circuits in section 5.1, a combination of basic circuits just may do the job. For example, if for an amplifier circuit

1.: high input impedance
2.: high voltage gain
3.: low output impedance

is required then — assuming an amplifier with BJTs — the

CEC can satisfy demand 2, and may be used for requirement 1
CBC can be used to achieve demand 2
CCC can satisfy demands 1 and 3.

From this it follows that all demands can be satisfied by cascading basic amplifier stages. Possible implementations that can be designed to meet all requirements include a CEC+CCC cascade (using two stages of amplifiers), and a CCC+CEC+CCC cascade, or a CEC+CBC+CCC cascade, or ... These latter three stage amplifiers can obviously achieve a higher overall voltage gain.

5.2.2 Cascading issues: signal transfer

The next figure shows a linear model of a capacitively coupled two-stage amplifier. The amplifier stages are reduced to their bare essence: only the most important parameters are included: the input impedance, output impedance and voltage gain or transconductance⁴¹ .

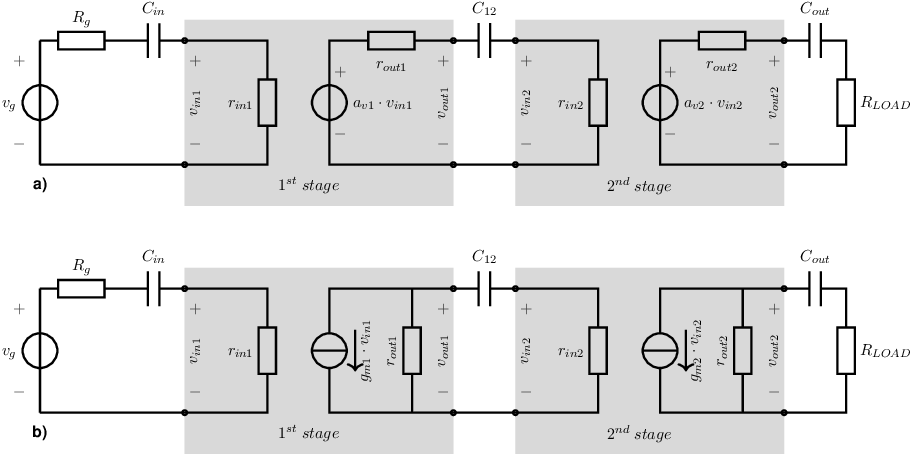
In the representation of a general two-stage amplifier, at both the input and output of each stage a coupling capacitor is included to avoid any possibility for clashing (DC) bias settings. This is however not always required: some basic amplifier stages can directly be coupled which may have advantages for bandwidth, power dissipation and (obviously) component count.

In calculating or deriving the overall properties of cascaded amplifiers, both the properties of the amplifiers themselves and the (signal transfer) effect of coupling needs to be taken into account. A few topics related to this are addressed below. Note that these (small signal) representations are heavily simplified: the input and output impedance of each stage is assumed to be resistive and the reverse isolation — the impact of the signals at the output port on the input port — is assumed to be zero.

5.2.3 Coupling capacitors: bandwidth limitations

Any coupling capacitor $C$ in combination with a resistive signal source or resistive load introduces a bandwidth limitation for the signal transfer. In the circuit representations in Figure 5.8 this holds for $C_{in}$ , $C_{12}$ and $C_{out}$ . The voltage signal transfer from $v_{g}$ to the actual input voltage as experienced by the first stage, $v_{in 1}$ , and from input voltage of a stage to its (loaded) output voltage are shown below, as is the overall transfer.

\begin{array}{rcl} H_{1} (jω) & = \frac{v_{in 1}}{v_{g}} = \frac{r_{in 1}}{r_{in 1} + Z_{Cin} + R_{g}} = \frac{r_{in 1}}{r_{in 1} + R_{g}} \cdot \frac{jω C_{in} (r_{in 1} + R_{g})}{1 + jω C_{in} (r_{in 1} + R_{g})} \\ H_{2} (jω) & = \frac{v_{in 2}}{v_{in 1}} = a_{v 1} \cdot \frac{r_{in 2}}{r_{in 2} + Z_{C 12} + r_{out 1}} = a_{v 1} \cdot \frac{r_{in 2}}{r_{in 2} + r_{out 1}} \cdot \frac{jω C_{12} (r_{in 2} + r_{out 1})}{1 + jω C_{12} (r_{in 2} + r_{out 1})} \\ H_{3} (jω) & = \frac{v_{out 2}}{v_{in 2}} = a_{v 2} \cdot \frac{R_{LOAD}}{R_{LOAD} + Z_{Cout} + r_{out 2}} = a_{v 2} \cdot \frac{R_{LOAD}}{R_{LOAD} + r_{out 2}} \cdot \frac{jω C_{out} (R_{LOAD} + r_{out 2})}{1 + jω C_{out} (R_{LOAD} + r_{out 2})} \\ H_{overall} (jω) & = \frac{v_{out 2}}{v_{g}} = H_{1} (jω) \cdot H_{2} (jω) \cdot H_{3} (jω) \end{array}

All signal transfers show a high-pass characteristic: the voltage gain is 0 for $ω = 0$ , while it has a constant non-zero value for $ω \to \infty$ . Characteristic parameters for a high pass filter are the “high frequency” signal transfer and the corner frequency:

\begin{array}{rcl} H_{1} (\infty) & = \frac{r_{in 1}}{r_{in 1} + R_{g}} f_{- 3 dB} = \frac{1}{2 π C_{in} (r_{in 1} + R_{g})} \\ H_{2} (\infty) & = a_{v 1} \cdot \frac{r_{in 2}}{r_{out 1} + r_{in 2}} f_{- 3 dB} = \frac{1}{2 π C_{12} (r_{in 2} + r_{out 1})} \\ H_{3} (\infty) & = a_{v 2} \cdot \frac{R_{LOAD}}{R_{LOAD} + r_{out 2}} f_{- 3 dB} = \frac{1}{2 π C_{out} (r_{out 2} + R_{LOAD})} \end{array}

Note that a voltage-voltage signal transfer is assumed. Getting the signal transfer for e.g. amplifier stages with a current-to-voltage signal transfer is straightforward. For all of these, the corner frequency is identical to the one derived above which can readily be seen using Norton-Thévenin equivalents. The actual transfer function is a little different but can be derived straightforwardly.

5.2.4 Maximizing gain

Above, an expression for the minimum attenuation when coupling amplifier stages, $H (\infty)$ , is shown when assuming both a source voltage and targeting an input voltage into the amplifier. The expressions for $H (\infty)$ are however different if this voltage-to-voltage transfer is not assumed. For example for an input current-to-voltage transfer $H {(\infty)}_{iv} = \frac{R_{in 1} \cdot R_{g}}{R_{in 1} + R_{g}}$ and for an input voltage-to-current transfer $H {(\infty)}_{vi} = \frac{1}{R_{in 1} + R_{g}}$ . For maximum gain it can readily be derived that

the -3dB corner frequency should be sufficiently below the lowest signal frequency
for voltage-to-voltage transfer $r_{in 1} > > R_{g}$ , where $R_{g}$ is relatively low-ohmic (voltage out)
for current-to-current transfer $r_{in 1} < < R_{g}$ , where $R_{g}$ is relatively high-ohmic (current out)
for current-to-voltage transfer $r_{in 1}$ and $R_{g}$ must be large, where $R_{g}$ is relatively high-ohmic (current out)
for voltage-to-current transfer $r_{in 1}$ and $R_{g}$ must be small, where $R_{g}$ is relatively low-ohmic (voltage out)

5.3 Other useful circuits

5.3.1 Voltage source

The most important property of a voltage source is its low output resistance. From table 1 and table 2 it follows that the emitter-follower (CCC) and source-follower (CDC) are the closest to a voltage source: they have the lowest $r_{out}$ of all basic amplifiers. Drive these circuits with a voltage source having a source resistance $R_{G}$ , then output resistance of the CCC and CDC is

\begin{array}{rcl} r_{out, CCC} = & R_{E} ∕ ∕ (\frac{β_{fe}}{g_{m}} + R_{g}) ∕ ∕ (\frac{\frac{β_{fe}}{g_{m}}}{\frac{β_{fe}}{g_{m}} + R_{g}}) \cdot \frac{1}{g_{m}} \\ r_{out, CDC} = & R_{S} ∕ ∕ \frac{1}{g_{m}} \end{array}

For both the CCC and the CDC, as a decent pessimistic approximation of the output resistance is then $r_{out} = 1 ∕ g_{m}$ . The circuit schematics below show such voltage source circuits, without coupling capacitors to be able to provide DC-voltages. Note that the resistors connecting to the base and gate are not required, but left here only to show the correspondence to the previously used CCCs and CDCs.

Voltage source with a low output resistance a) with a CCC (NPN) b) with a CDC (NMOS)

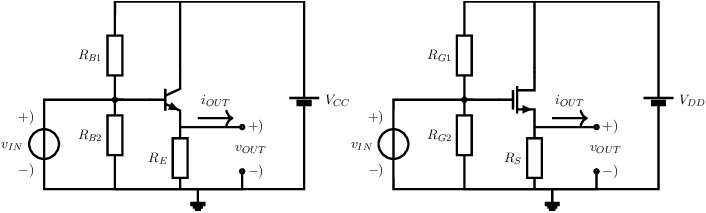
It may be clear that (large signal wise) $v_{OUT} = v_{IN} - v_{BE} (I_{C} + i_{OUT})$ respectively $v_{OUT} = v_{IN} - v_{GS} (I_{D} + i_{OUT})$ for these two circuits: there is a bias current dependent difference between $v_{IN}$ and $v_{OUT}$ and there is a load current-dependent voltage difference. For $i_{OUT} < < I_{BIAS}$ this translates into the forenamed small signal output resistance $r_{out} \approx 1 ∕ g_{m}$ . Note that the circuits can source ( $i_{OUT} > 0$ ) currents that are substantially larger than the bias current, wile they cannot sink ( $i_{OUT} < 0$ ) currents larger than the bias current.

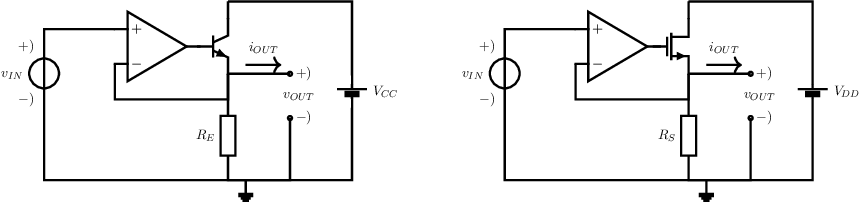
The offset-issue and the limited output resistance (for $i_{OUT} > 0$ ) can both be solved by applying feedback. This may lead to e.g. the following circuit schematics. The fact that this circuit cannot sink (significant) currents can be solved by adding its P-type complement.

Improved voltage source circuit schematics

5.3.2 Current source

An ideal current source has an infinite output resistance. A good starting point for the design of a real current source would be a basic circuit that already has a relatively high output resistance: a CEC with emitter degeneration or a CSC with source degeneration. To derive equations for output resistance, we must take the output resistance of the transistor, $μ ∕ g_{m}$ into account.

Simple current source implementations, with a BJT, with an NMOS and the SSEC of the bipolar version

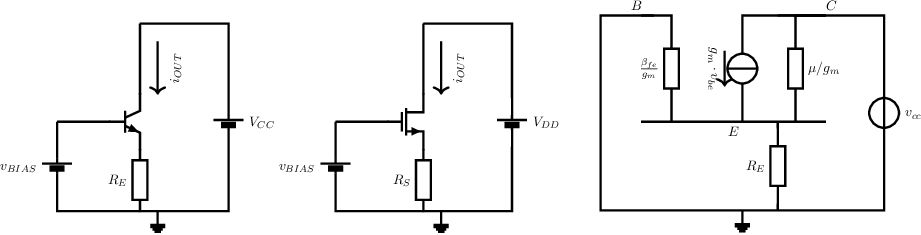
The bias current for both circuits in the figure is determined by the (impedance of the) bias source at the input, the degeneration resistor and the characteristics of the transistor. For a current source, this current has to be as constant as possible: the output resistance must be as large as possible. Using the SSEC it can be derived that (for the BJT case):

\begin{array}{rcl} r_{out} = \frac{v_{cc}}{i_{c}} \\ i_{c} = g_{m} \cdot v_{be} + \frac{v_{cc} - v_{E}}{μ ∕ g_{m}} \\ v_{be} = - v_{E} \\ v_{E} = i_{c} \cdot (\frac{β_{fe}}{g_{m}} ∕ ∕ R_{E}) \\ r_{out} = \frac{μ}{g_{m}} + (μ + 1) \cdot (\frac{β_{fe}}{g_{m}} ∕ ∕ R_{E}) \end{array}

The output resistance of the circuit is the sum of the output resistance of the transistor and the multiplied degeneration resistor (for the NMOS-version you can set $β_{fe} \to \infty$ ). Pretty much the same as for the voltage source circuitry in §5.3.1, addition of a feedback loop with an opamp can significantly increase the output impedance.

5.3.3 Current mirror

For a number of applications (in circuits) a sort of copy-circuit comes in handy, for example for re-using or distributing signals or bias settings. For copying a voltage, we can use a unity voltage gain voltage buffer⁴². To get multiple copies of a specific DC current, multiple current sources as described in section 5.3.2 may be used. In this case, the $V_{BIAS}$ voltage source may be re-used to drive multiple current source circuits which pushes down circuit complexity.

Another very useful circuit is one that makes an actual copy from some input current. Noting that the current-voltage relation of a transistor is monotonous, a convenient method to achieve this is:

create for a transistor a (gate-source or base-emitter) voltage that corresponds, for that transistor, to a (drain or collector) current equal to the input current.
- for a BJT with $i_{C} = f (v_{BE})$ this would be $v_{BE} = f^{- 1} (i_{C})$
- for an MOS transistor with $i_{D} = f (v_{GS})$ this would be $v_{GS} = f^{- 1} (i_{D})$
use that voltage to drive similar transistors to get a copy of the input current
- for a BJT we then get $i_{C, out} = f (f^{- 1} (i_{C, in})) = i_{C, in}$ and
- for an MOS transistor you get $i_{D, out} = f (f^{- 1} (i_{D, in})) = i_{D, in}$

A number of circuit that implement this is shown below; in these circuit schematics, it is assumed that the output current can flow into some node. These circuits are called current mirrors .

Some current mirror circuits

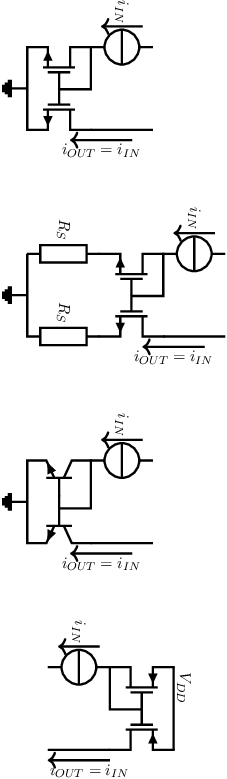
Again, the value of the degeneration resistance can be chosen freely: they influence both the output resistance and the required voltage headroom. Obviously, we can also create current mirrors with PMOS transistors and PNPs. Even more so, any active element with an arbitrary monotone function between output current and input voltage will do for a current mirror. A number of characteristics of current mirrors are calculated below.

The small signal current transfer can be derived from a small-signal equivalent circuit of third current mirror, neglecting the transistor’s output resistance:

\begin{array}{rcl} H = \frac{i_{c 2}}{i_{in}} \\ i_{c 2} = g_{m 2} \cdot v_{be 2} \\ v_{be 2} = v_{be 1} \\ v_{be 1} = i_{in} \cdot (\frac{1}{g_{m 1}} ∕ ∕ \frac{{β_{fe}}_{1}}{g_{m 1}} ∕ ∕ \frac{{β_{fe}}_{2}}{g_{m 2}}) \\ H = g_{m 2} \cdot (\frac{1}{g_{m 1}} ∕ ∕ \frac{{β_{fe}}_{1}}{g_{m 1}} ∕ ∕ \frac{{β_{fe}}_{2}}{g_{m 2}}) \end{array}

If both transistors are identical, with the same $β_{fe}$ and $I_{C 0}$ , then the relation simplifies to

\begin{array}{rcl} H & = g_{m} \cdot (\frac{1}{g_{m}} ∕ ∕ \frac{β_{fe}}{g_{m}} ∕ ∕ \frac{β_{fe}}{g_{m}}) = \frac{β_{fe}}{β_{fe} + 2} \end{array}

For the large signal current transfer:

\begin{array}{rcl} H = \frac{i_{C 2}}{i_{IN}} \\ i_{C 2} = I_{C 0, 2} \cdot e^{\frac{q \cdot v_{B} E}{kT}} \\ v_{BE} = \frac{kT}{q} \cdot \ln (\frac{i_{C 1}}{I_{C 0, 1}}) \\ i_{C 1} = i_{IN} - i_{B 1} - i_{B 2} = i_{IN} - \frac{i_{C 1}}{{β_{fe}}_{1}} - \frac{i_{C 2}}{{β_{fe}}_{2}} \\ H = \frac{\frac{I_{C 0, 2}}{I_{C 0, 1}}}{1 + \frac{I_{C 0, 2}}{I_{C 0, 1}} \cdot \frac{1}{{β_{fe}}_{2}} + \frac{1}{{β_{fe}}_{1}}} \end{array}

Yet again, this is an ugly bugger, though the large-signal current transfer is linear because the nonlinear element equation for the BJT is used in combination with its inverse. This equation can be simplified further if we assume identical transistors:

\begin{array}{rcl} H & = \frac{β_{fe}}{β_{fe} + 2} \end{array}

This result can also readily be derived noting that for identical BJTs operated on the same $v_{BE}$ the collector currents are equal. Noting that the input current consists of the collector current and two base currents whereas the output current is only the collector current leads to $H = \frac{β_{fe}}{β_{fe} + 2}$ . For unequal transistors, we get a non-unity current gain factor; this can be very useful in some circuits.

[prev] [prev-tail] [front] [up]