Exercise 5.2 A weird degenerated amplifier with an NPN

a)

An answer:
Bias = DC $\to$, $C=\mathit{open}$, $L=\mathit{short}$ and assume $V_{\mathit{BE}}\approx 0.6V$

$$\begin{array}{rcll}& I_C& =\mathit{\beta fe}{I}_B& \\ & & I_B=\frac{V_{\mathit{CC}}-V_B}{R_B}& \\ & & V_B=\left(1+\frac{1}{\mathit{\beta fe}}\right)I_C{R}_E+0.6V& \\ & & I_B=\frac{V_{\mathit{CC}}-\left(1+\frac{1}{\mathit{\beta fe}}\right)I_C{R}_E-0.6V}{R_B}& \\ & I_C& =\mathit{\beta fe}\cdot \frac{V_{\mathit{CC}}-\left(1+\frac{1}{\mathit{\beta fe}}\right)I_C{R}_E-0.6V}{R_B}& \end{array}$$

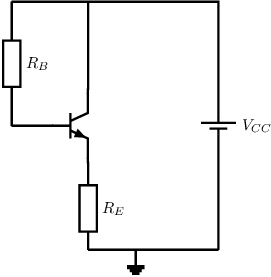
This requires some rewriting: separation of variables to get a closed expression for $I_C$:

$$\begin{array}{rcll}& & I_C\left(1+\frac{(1+\mathit{\beta fe})R_E}{R_B}\right)=\frac{\mathit{\beta fe}(V_{\mathit{CC}}-0.6V)}{R_B}⟹& \\ & I_C& =\frac{\mathit{\beta fe}(V_{\mathit{CC}}-0.6V)}{R_B\left(1+\frac{(1+\mathit{\beta fe})R_E}{R_B}\right)}& \\ & & =\frac{\mathit{\beta fe}(V_{\mathit{CC}}-0.6V)}{R_B+(1+\mathit{\beta fe})R_E}& \end{array}$$

b)

An answer:
The voltage drop across $L_1$ is zero (short at DC), so $V_C=V_{\mathit{CC}}$. Or you can see it directly from the equivalent circuit for operation at DC in the previous answer.

c)

An answer:
A common emitter circuit (CEC)

d)

An answer:
You can ignore the output impedance of the transistor as long as it is significantly higher than other impedances at the relevant node (collector). In this case that means that $Z_{L1}<<Z_{\mathit{out},\mathit{BJT}}$ for signal frequencies.

e)

An answer:
Set DC sources to 0 (in this circuit that is only $V_{\mathit{CC}}$). Assume that the values of reactances for which no values are specified are large. Note that in this exercise you have to retain $C_{\mathit{in}}$ and $C_1$! This allows to replace them by shorts or opens: $L_1\to$open, $C_E\to$short, $C_{\mathit{out}}\to$short.

SSEC of the BJT (including B/C/E node identifiers)

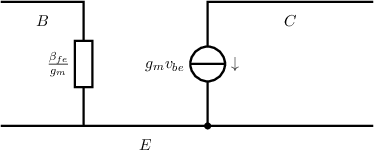
Indicate $v_{\mathit{in}}$ and $v_{\mathit{out}}$ and redraw. Again: you should (see the description of the circuit) not replace $C_{\mathit{in}}$, $C_1$ by shorts!

f)

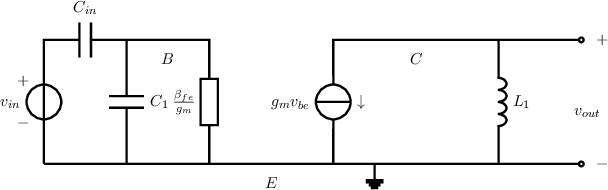
An answer:
In this answer, the output port is driven from an independent voltage source driving the output port. The other independent sources need to be set to zero. The corresponding small signal equivalent circuit is given below. This will be used to derive $z_{\mathit{out}}=\frac{v_{\mathit{out}}}{i_{\mathit{out}}}$.

$$\begin{array}{rcll}& z_{\mathit{out}}& =\frac{v_{\mathit{out}}}{i_{\mathit{out}}}& \\ & & i_{\mathit{out}}=i_{L1}+g_m{v}_{\mathit{be}}& \\ & & v_{\mathit{be}}=0& \\ & & i_{L2}=\frac{v_{\mathit{out}}}{\mathit{j\omega }{L}_1}& \\ & z_{\mathit{out}}& =\frac{v_{\mathit{out}}}{i_{\mathit{out}}}=\mathit{j\omega }{L}_1& \end{array}$$

g)

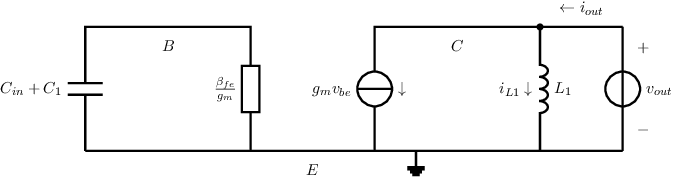
An answer:
Using the SSEC from question e) to calculate the voltage gain $a_v=\frac{v_{\mathit{out}}}{v_{\mathit{in}}}$ can be done as follows.

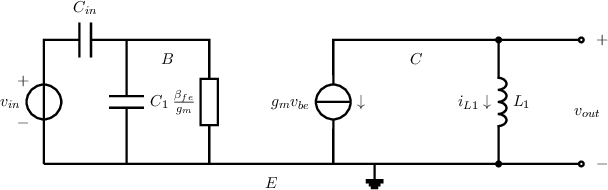
This SSEC can be simplified by capturing $C_1$ and $\mathit{\beta fe}∕g_m$ into one impedance

$$\begin{array}{rcll}{Z}_B& =\frac{\frac{\mathit{\beta fe}}{g_m}\cdot \frac{1}{\mathit{j\omega }{C}_1}}{\frac{\mathit{\beta fe}}{g_m}+\frac{1}{\mathit{j\omega }{C}_1}}& & \\ & =\frac{\frac{\mathit{\beta fe}}{g_m}}{1+\mathit{j\omega }{C}_1\frac{\mathit{\beta fe}}{g_m}}& & \end{array}$$

A derivation can be done as shown below:

$$\begin{array}{rcll}& a_v& =\frac{v_{\mathit{out}}}{v_{\mathit{in}}}& \\ & & v_{\mathit{out}}=i_{L1}\mathit{j\omega }{L}_1& \\ & & i_{L1}=-g_m{v}_{\mathit{be}}& \\ & & v_{\mathit{be}}=v_B& \\ & & v_B=\frac{Z_B}{Z_B+Z_{C_{\mathit{in}}}}\cdot v_{\mathit{in}}& \end{array}$$

Now back substitution leads to the/an answer:

$$\begin{array}{rcll}& & v_B=\frac{Z_B}{Z_B+Z_{C_{\mathit{in}}}}\cdot v_{\mathit{in}}& \\ & & =\frac{\frac{\frac{\mathit{\beta fe}}{g_m}}{1+\mathit{j\omega }{C}_1\frac{\mathit{\beta fe}}{g_m}}}{\frac{\frac{\mathit{\beta fe}}{g_m}}{1+\mathit{j\omega }{C}_1\frac{\mathit{\beta fe}}{g_m}}+\frac{1}{\mathit{j\omega }{C}_{\mathit{in}}}}\cdot v_{\mathit{in}}& \\ & & =\frac{\mathit{j\omega }{C}_{\mathit{in}}\frac{\mathit{\beta fe}}{g_m}}{1+\mathit{j\omega }\frac{\mathit{\beta fe}}{g_m}(C_1+C_{\mathit{in}})}\cdot v_{\mathit{in}}& \end{array}$$

$$\begin{array}{rcll}& v_{\mathit{out}}& =-g_m{v}_B\cdot \mathit{j\omega }{L}_1& \\ & & =\mathit{j\omega }{L}_1{g}_m\frac{\mathit{j\omega }{C}_{\mathit{in}}\frac{\mathit{\beta fe}}{g_m}}{1+\mathit{j\omega }\frac{\mathit{\beta fe}}{g_m}(C_1+C_{\mathit{in}})}\cdot v_{\mathit{in}}& \\ & a_v& =-\frac{v_{\mathit{out}}}{v_{\mathit{in}}}& \\ & & =\frac{{(\mathit{j\omega })}^2\mathit{\beta fe}{L}_1{C}_{\mathit{in}}}{1+\mathit{j\omega }\frac{\mathit{\beta fe}}{g_m}(C_1+C_{\mathit{in}})}& \\ & & =-\frac{{(\mathit{j\omega })}^2\mathit{\beta fe}{L}_1{C}_{\mathit{in}}}{1+\mathit{j\omega }\frac{\mathit{\beta fe}}{g_m}(C_1+C_{\mathit{in}})}& \end{array}$$