Exercise 5.1 An amplifier with 2 outputs

a)

An answer:
As a first guess, let’s neglect the base current, derive the value for $R_{B1}$ for that assumption and after that determine whether this assumption was valid. From the exercise we can readily get a number of currents and voltages:

$$\begin{array}{rcll}& & V_B=\frac{R_{B2}}{R_{B1}+R_{B2}}\cdot V_{\mathit{CC}}\to & \\ & & R_{B1}=\frac{R_{B2}\cdot (V_{\mathit{CC}}-V_B)}{V_B}& \end{array}$$

$$\begin{array}{rcll}& I_E=1\mathit{mA}& & \\ & R_E=500\mathrm{\Omega }& & \\ & V_E=0.5V& & \\ & V_{\mathit{BE}}=0.6& & \\ & V_B=1.1V& & \end{array}$$

$$\begin{array}{rcll}& R_{B1}& =\frac{R_{B2}\cdot (V_{\mathit{CC}}-V_B)}{V_B}& \\ & & =\frac{220k\mathrm{\Omega }\cdot (5-1.1)}{1.1}& \\ & & =780k\mathrm{\Omega }& \end{array}$$

Neglecting base current may be valid but this must be checked. ONLY if the base current $I_B$ is much smaller than the current in $R_{B1}$ the assumption was/is valid.

$$\begin{array}{rcll}& I_B& =\frac{I_E}{\mathit{\beta fe}+1}=10\mathit{\mu A}& \\ & I_{B2}& =\frac{V_B}{R_{B2}}& \\ & & =\frac{1.1V}{220k\mathrm{\Omega }}& \\ & & =5\mathit{\mu A}=\frac{1}{2}{I}_B& \end{array}$$

As $I_B$ is not much smaller than $I_{\mathit{RB}2}$, the base current cannot be ignored. Therefore a more elaborate derivation much be done taking the impact of $I_B$ into account!

$$\begin{array}{rcll}& R_{B1}& =\frac{V_{R_{B1}}}{I_{B1}}& \\ & & I_{R_{B1}}=I_B+I_{R_{B2}}& \\ & & V_{R_{B1}}=V_{\mathit{CC}}-V_B& \\ & & I_{R_{B2}}=\frac{V_B}{R_{B2}}& \\ & R_{B1}& =\frac{3.9}{0.015\cdot 10^{-3}}=260k\mathrm{\Omega }& \end{array}$$

b)

An answer:
There is (negative) feedback that serves to stabilize the bias settings. This can conveniently be explained using a type of flow diagram:

$$\begin{array}{rcll}& I_C& =I_{C0}(T)\cdot e^{\frac{q{V}_{\mathit{BE}}}{\mathit{KT}}}& \\ & & T\uparrow \to & \\ & & I_C\uparrow \to & \\ & & V_E\uparrow \mathit{and}{V}_B\downarrow \to & \\ & & V_{\mathit{BE}}\downarrow \to & \\ & & I_C\downarrow & \end{array}$$

whereby the $\uparrow$ indicates an increase and the $\downarrow$ indicates a decrease in value.

c)

An answer:
$$\begin{array}{rcll}& g_m& \equiv \frac{\partial i_C}{\partial v_{\mathit{BE}}}& \\ & & =\frac{q}{\mathit{kT}}{I}_C& \\ & & \approx 40\cdot I_C& \\ & & =40\cdot 10^{-3}=0.04A∕V& \\ & \frac{\mathit{\beta fe}}{g_m}& =\frac{99}{0.04}=2475\mathrm{\Omega }& \end{array}$$

d)

An answer:

e)

An answer:

$$\begin{array}{rcll}& v_{\mathit{out}1}& =-i_c\cdot R_C& \\ & v_{\mathit{out}2}& =i_e\cdot R_E& \\ & & =\frac{\mathit{\beta fe}+1}{\mathit{\beta fe}}{i}_c\cdot R_E& \\ & \mathit{with}& \mathit{\beta fe}>>1\to & \\ & & I_C\approx I_E\to & \\ & & R_C\approx R_E=500\mathrm{\Omega }& \end{array}$$

f)

An answer:

$$\begin{array}{rcll}& v_{\mathit{out}1}& =-i_c\cdot R_C& \\ & v_{\mathit{out}2}& =i_e\cdot R_E=\frac{\mathit{\beta fe}+1}{\mathit{\beta fe}}{i}_c\cdot R_E& \\ & v_{\mathit{out}2}& =-v_{\mathit{out}1}\cdot \frac{\mathit{\beta fe}+1}{\mathit{\beta fe}}\mathrm{\text{ (signals are in antiphase)}}& \end{array}$$

g)

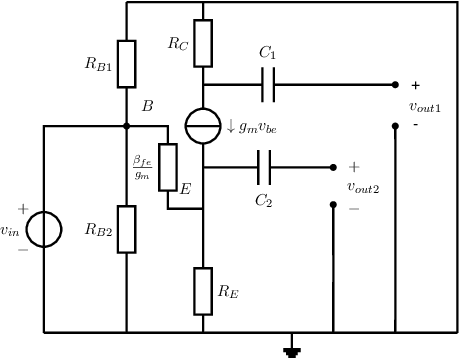
An answer:
The (unloaded) output voltage $v_{\mathit{out}2}$ due to $v_{\mathit{in}}$ is:

$$\begin{array}{rcll}& v_{\mathit{out}2}& =R_E\cdot I_{R_E}& \\ & & =R_E\left(\frac{v_{\mathit{be}}}{\mathit{\beta fe}∕g_m}+g_m{v}_{\mathit{be}}\right)& \\ & & =g_m{R}_E\left(\frac{1}{\mathit{\beta fe}}+1\right)v_{\mathit{be}}& \\ & & v_{\mathit{be}}=v_b-v_e& \\ & & b_{\mathit{be}}=v_{\mathit{in}}-v_{\mathit{out}1}& \\ & v_{\mathit{out}2}& =g_m{R}_E\left(\frac{1}{\mathit{\beta fe}}+1\right)\left(v_{\mathit{in}}-v_{\mathit{out}1}\right)& \\ & & =\frac{g_m{R}_E\left(\frac{1}{\mathit{\beta fe}}+1\right)}{1+g_m{R}_E\left(\frac{1}{\mathit{\beta fe}}+1\right)}\cdot v_{\mathit{in}}& \end{array}$$

The next step is to calculate the short circuit output current due to $v_{\mathit{in}}$ - for this we need a new small signal equivalent circuit:

$$\begin{array}{rcll}& i_{\mathit{out}2}& =\frac{v_{\mathit{in}}}{\mathit{\beta fe}∕g_m}+g_m{v}_{\mathit{be}}& \\ & & =v_{\mathit{in}}\left(\frac{g_m}{\mathit{\beta fe}}+g_m\right)& \\ & & =v_{\mathit{in}}\left(\frac{1}{\mathit{\beta fe}}+1\right)\cdot g_m& \end{array}$$

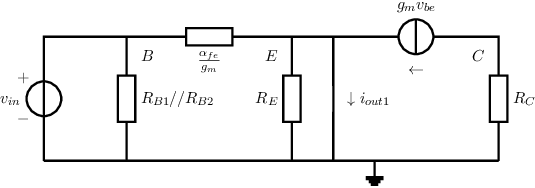
Note that for this SSEC, $v_{\mathit{be}}=v_{\mathit{in}}$ because $R_E$ appears shorted

$$\begin{array}{rcll}& r_{\mathit{out}}& =\frac{v_{\mathit{out}1}}{i_{\mathit{out}1}}& \\ & & =\frac{\frac{g_m{R}_E\left(\frac{1}{\mathit{\beta fe}}+1\right)}{1+g_m{R}_E\left(\frac{1}{\mathit{\beta fe}}+1\right)}\cdot v_{\mathit{in}}}{\left(\frac{1}{\mathit{\beta fe}}+1\right)g_m{v}_{\mathit{in}}}& \\ & & =\frac{R_E}{1+g_m{R}_E\left(\frac{1}{\mathit{\beta fe}}+1\right)}& \end{array}$$

h)

An answer:

$$\begin{array}{rcll}& i_{\mathit{in}}& =\frac{v_{\mathit{in}}}{R_{B_1}∕∕R_{B_2}}+\frac{v_{\mathit{be}}}{\mathit{\beta fe}∕g_m}& \\ & & v_{\mathit{be}}=v_{\mathit{in}}-v_{\mathit{out}1}& \\ \to i_{\mathit{in}}& =\frac{v_{\mathit{in}}}{R_{B_1}∕∕R_{B_2}}+\frac{v_{\mathit{in}}-\frac{g_m{R}_E\left(\frac{1}{\beta \mathit{fe}}+1\right)}{1+g_m{R}_E\left(\frac{1}{\beta \mathit{fe}}+1\right)}\cdot v_{\mathit{in}}}{\mathit{\beta fe}∕g_m}& & \\ & =\frac{v_{\mathit{in}}}{R_{B_1}∕∕R_{B_2}}+v_{\mathit{in}}\cdot \frac{g_m}{\mathit{\beta fe}}\cdot \left(1-\frac{g_m{R}_E\left(\frac{1}{\mathit{\beta fe}}+1\right)}{1+g_m{R}_E\left(\frac{1}{\mathit{\beta fe}}+1\right)}\right)& & \\ & =\frac{v_{\mathit{in}}}{R_{B_1}∕∕R_{B_2}}+v_{\mathit{in}}\cdot \frac{g_m}{\mathit{\beta fe}}\cdot \frac{1}{1+g_m{R}_E\left(\frac{1}{\mathit{\beta fe}}+1\right)}& & \\ & =\frac{v_{\mathit{in}}}{R_{B_1}∕∕R_{B_2}}+\frac{v_{\mathit{in}}}{\frac{\mathit{\beta fe}}{g_m}+R_E(1+\mathit{\beta fe})}& & \\ \to r_{\mathit{in}}& =R_{B_1}∕∕R_{B_2}∕∕\left(\frac{\mathit{\beta fe}}{g_m}+R_E(1+\mathit{\beta fe})\right)& & \end{array}$$

Reusing a previous equation for $v_{\mathit{out}1}(v_{\mathit{in}})$ can shorten the derivation (only) a little. This leads to

$$\begin{array}{rcll}& i_{\mathit{in}}& =\frac{v_{\mathit{in}}}{R_{B_1}∕∕R_{B_2}}+\frac{v_{\mathit{in}}-\frac{g_m{R}_E\left(\frac{1}{\mathit{\beta fe}}+1\right)}{1+g_m{R}_E\left(\frac{1}{\mathit{\beta fe}}+1\right)}\cdot v_{\mathit{in}}}{\mathit{\beta fe}∕g_m}& \\ & & =\frac{v_{\mathit{in}}}{R_{B_1}∕∕R_{B_2}}+v_{\mathit{in}}\cdot \frac{g_m}{\mathit{\beta fe}}\cdot \left(1-\frac{g_m{R}_E\left(\frac{1}{\mathit{\beta fe}}+1\right)}{1+g_m{R}_E\left(\frac{1}{\mathit{\beta fe}}+1\right)}\right)& \\ & & =\frac{v_{\mathit{in}}}{R_{B_1}∕∕R_{B_2}}+v_{\mathit{in}}\cdot \frac{g_m}{\mathit{\beta fe}}\cdot \frac{1}{1+g_m{R}_E\left(\frac{1}{\mathit{\beta fe}}+1\right)}& \\ & & =\frac{v_{\mathit{in}}}{R_{B_1}∕∕R_{B_2}}+\frac{v_{\mathit{in}}}{\frac{\mathit{\beta fe}}{g_m}+R_E(1+\mathit{\beta fe})}& \\ & r_{\mathit{in}}& =R_{B_1}∕∕R_{B_2}∕∕\left(\frac{\mathit{\beta fe}}{g_m}+R_E(1+\mathit{\beta fe})\right)& \end{array}$$