Exercise 5.3 A common-collector amplifier

a)

An answer:

$$\begin{array}{rcll}& R_E& =\frac{V_E}{I_E}& \\ & & V_E=V_B-V_{\mathit{BE}}& \\ & & I_E=\frac{\mathit{\beta fe}+1}{\mathit{\beta fe}}{I}_C& \end{array}$$

$V_B$ is the voltage at the base node, which generally cannot be calculated merely assuming $R_{B1}$ and $R_{B2}$ form a resistive divider and hence applying the formula for that. This can easily be seen in the circuit schematic depicting the voltages and currents at and around $R_{B1}$ and $R_{B2}$.

From this $V_B$ can be derived. Formulating KCL/KVL:

$$\begin{array}{rcll}& \frac{V_B}{R_{B2}}+\frac{V_B-V_{\mathit{CC}}}{R_{B1}}-I_C∕\mathit{\beta fe}=0& & \end{array}$$

leading to

$$\begin{array}{rcll}& R_{B1}{V}_B+R_{B2}{V}_B-R_{B2}{V}_{\mathit{CC}}+R_{B1}{R}_{B2}{I}_B=0⟹& & \\ & V_B=\frac{R_{B2}{V}_{\mathit{CC}}-R_{B1}{R}_{B2}{I}_B}{R_{B1}+R_{B2}}& & \end{array}$$

Or applying superposition you get the same equation in a different appearance:

$$V_B=V_{\mathit{CC}}\frac{R_{B2}}{R_{B1}+R_{B2}}-I_B\frac{R_{B1}{R}_{B2}}{R_{B1}+R_{B2}}$$

This yields:

$$R_E=\frac{V_{\mathit{CC}}\frac{R_{B2}}{R_{B1}+R_{B2}}+I_B\frac{R_{B1}{R}_{B2}}{R_{B1}+R_{B2}}-V_{\mathit{BE}}}{\frac{\mathit{\beta fe}+1}{\mathit{\beta fe}}{I}_C}$$

This yields numerically

$$\begin{array}{rcll}& & V_B=4V& \\ & & V_{\mathit{BE}}=0.7V& \\ & & R_E=330\mathrm{\Omega }& \end{array}$$

b)

An answer:
When the signals are sufficiently small so that we can approximate the non-linear transistor characteristics by a linear function.

c)

An answer:

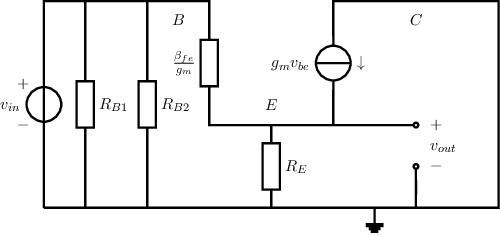
Which can be redrawn (simplified) into

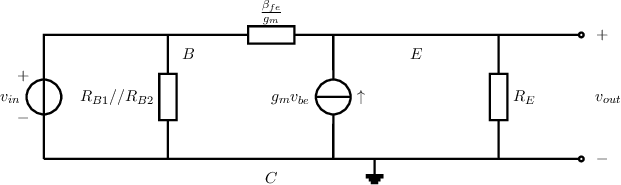
To calculate the output resistance, e.g set $v_{\mathit{in}}=0$ and force a voltage at the output $v_{\mathit{out},\mathit{forced}}$. Then calculate the current delivered by $v_{\mathit{out},\mathit{forced}}$ and apply Ohm’s law.

$$\begin{array}{rcll}& r_{\mathit{out}}& =\frac{v_{\mathit{out},\mathit{forced}}}{i_{\mathit{out}}}& \\ & & i_{\mathit{out}}=\frac{v_{\mathit{out},\mathit{forced}}}{R_E}+\frac{v_{\mathit{out},\mathit{forced}}}{\mathit{\beta fe}∕g_m}-g_m\cdot v_{\mathit{be}}& \\ & & i_{\mathit{out}}=\left(\frac{1}{R_E}+\frac{g_m}{\mathit{\beta fe}}+g_m\right)\cdot v_{\mathit{out},\mathit{forced}}& \\ & r_{\mathit{out}}& =R_E∕∕\frac{\mathit{\beta fe}}{g_m}∕∕\frac{1}{g_m}& \end{array}$$