Exercise 11.3 Impedances from reactances

In physical realizations of RF circuits, capacitors with some kind of leads are used. The capacitor value is $C$, the length of the lead wires is $l$ mm on each side of the capacitor. Assume that the inductance per length is $L=2\mathit{nH}∕\mathit{mm}$.

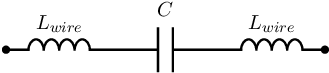
a)

Derive an equation for the impedance of the capacitor with wires, $Z_{\mathit{cap}}(\mathit{j\omega })$, at (radian) frequency $\omega$.

b)

Assuming that $C=50\mathit{pF}$ and lead wires of 1 cm at each side of the capacitor. Derive the impedance of the capacitor with wires at 100 MHz.

c)

Derive the value of the apparent —or net — capacitance of the 50 pF capacitor with 1 cm wires in the previous question, at 100 MHz.

d)

Draw the impedance of the base capacitor, and of the total wire length in the impedance plane (2-dimensional, $\mathit{Re}(Z)$) on the x-axis, $\mathit{Im}(Z)$ on the y-axis. From this construct the net capacitance graphically.

e)

Derive the value of the apparent —or net — capacitance of a 10 pF capacitor with 1 cm wires in the previous question, at 100 MHz.

f)

Derive the value of the apparent —or net — capacitance of a 1 nF capacitor with 1 cm wires in the previous question, at 100 MHz.

g)

Assuming that the target net capacitance is 100 pF and that lead wires are 1 cm on each side, derive the capacitance value (without leads) required to get that 100 pF, again at 100 MHz.