Exercise 9.15 An harmonic oscillator with all pass sections?

Given is the circuit below; this circuit is intended to be an harmonic oscillator.

• The opamps are ideal, with a real valued voltage gain $A\to \infty$ and with no frequency dependency.
• The value of all resistors is the same ($R$). All capacitors have identical values ($C$).

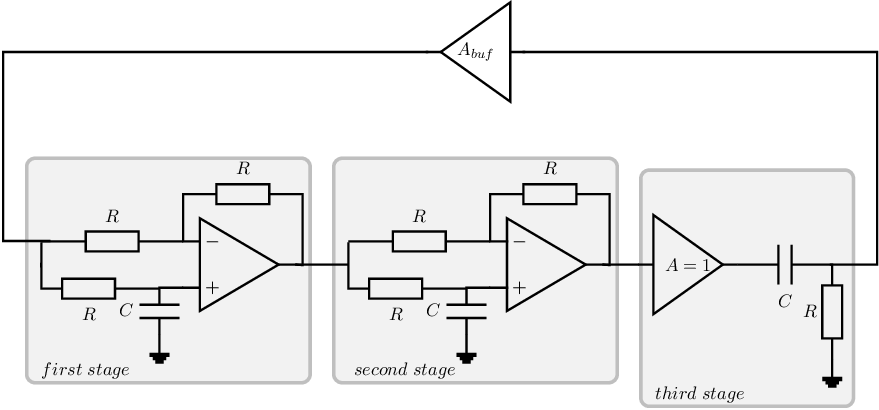
(a)

Which condition(s) must be satisfied to get harmonic oscillation?

The circuit can be decomposed into 3 stages that have frequency dependent transfer functions (identified by their gray background in the figure), and one ideal voltage buffer stage with a real valued voltage gain $A_{\mathit{buf}}$.

(b)

Show (with a derivation) that the voltage transfer for both the first stage and for the second stage is $H(\mathit{j\omega })=\frac{1-\mathit{j\omega RC}}{1+\mathit{j\omega RC}}$.

(c)

Derive the phase shift of each of the three stages for $\omega =0$ and for $\omega \to \infty$(rad/s). Note that your answer consists of six phases, two per stage.

(d)

Draw in one Bode plot (magnitude and phase) the voltage transfer of each of the three stages. You may assume (for this plot) $R=1\mathrm{\Omega }$ and $C=1F$.

(e)

Determine whether the given circuit can function as harmonic oscillator using a positive $A_{\mathit{buf}}$. If your answer shows that harmonic oscillation can be possible, derive an expression for the (radian) oscillation frequency and for the required $A_{\mathit{buf}}$. Otherwise demonstrate clearly (mathematically) that this circuit cannot oscillate harmonically.

Explicit hint: using the findings in the previous 2 questions or using standard forms for transfer functions simplifies significantly.

(f)

Determine whether the given circuit can function as harmonic oscillator using a negative $A_{\mathit{buf}}$. If your answer shows that harmonic oscillation can be possible, derive an expression for the (radian) oscillation frequency and for the required $A_{\mathit{buf}}$. Otherwise demonstrate clearly (mathematically) that this circuit cannot oscillate harmonically.

Explicit hint, the same one: using the findings in the previous 2 questions or using standard forms for transfer functions simplifies significantly.