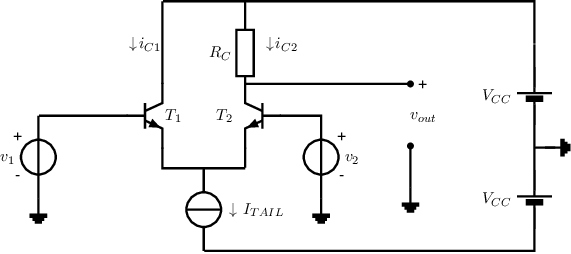
Exercise 8.4 A differential pair

In the circuit, the two BJTs in the differential pair ($T_1$ and $T_2$) are identical. The transistors can be assumed to operate in active forward, for which $v_{\mathit{CE}}>0.1V$. In this operating region, the output resistance $r_{\mathit{ce}}$ of the BJTs can be assumed to be infinitely large. Furthermore, $i_C=I_{C0}\cdot e^{\frac{q{v}_{\mathit{BE}}}{\mathit{kT}}}$, the current gain $\mathit{\beta fe}$ is finite and much larger than unity, $V_{\mathit{CC}}=5V$, $I_{\mathit{TAIL}}=1\mathit{mA}$, $R_C=4.7k\mathrm{\Omega }$ and $\mathit{kT}∕q=25\mathit{mV}$.

a)

Assume that the base of $T_2$ is connected to ground ($v_2=0V$). Derive a relation between the common-mode input signal $v_{\mathit{in},\mathit{cm}}$ and $v_1$.

b)

Assuming that $v_1=v_2=0V$, derive expressions for the collector currents of the two BJTs.

c)

Derive (or approximate) the value of $v_1$ in order to get $I_{C2}=0.05I_{\mathit{TAIL}}$, for $v_2=0$.

d)

Derive (or approximate) the value of $v_1$ in order to get $I_{C2}=0.95I_{\mathit{TAIL}}$, for $v_2=0$.

e)

Estimate the (absolute) maximum voltage swing across $R_C$.

f)

Estimate the (absolute) minimum value of $v_{\mathit{CB}}$ of $T_2$.

g)

Derive an expression for the slew-rate of the circuit in case there is a capacitor $C_M$ in parallel with $R_C$. Calculate the numerical value of the slew-rate for $C_M=100\mathit{pF}$.

h)

Derive an expression for the small-signal voltage gain $a_v=v_{\mathit{out}}∕v_1$.

i)

Using a feedback network, we now set $v_2=\beta \cdot v_{\mathit{out}}$. Derive an expression for the differential input voltage of the circuit ($v_1-v_2$) as a function of $v_1$. in the derivation, you may use the fact that the (small signal) voltage gain $a_v$ is known: that was derived in the previous question.