Exercise 9.15 An harmonic oscillator with all pass sections?

(a)

The circuit can be decomposed into 3 stages that have frequency dependent transfer functions (identified by their gray background in the figure), and one ideal voltage buffer stage with a real valued voltage gain $A_{\mathit{buf}}$.

(b)

An answer:
see 6, question Exercise 6.7 .

(c)

An answer:

$$\begin{array}{lllllll}\hfill & \angle H_1(j0)=0^{\circ }& \hfill \angle H_1(j\infty )=-180^{\circ }& & \hfill & & \hfill \\ \hfill & \angle H_2(j0)=0^{\circ }& \hfill \angle H_2(j\infty )=-180^{\circ }& & \hfill & & \hfill \\ \hfill & \angle H_3(j0)=90^{\circ }& \hfill \angle H_3(j\infty )=0^{\circ }& & \hfill & & \hfill \end{array}$$

(d)

An answer:
Using the specified R and C and using $\omega =1∕\mathit{RC}$:

(e)

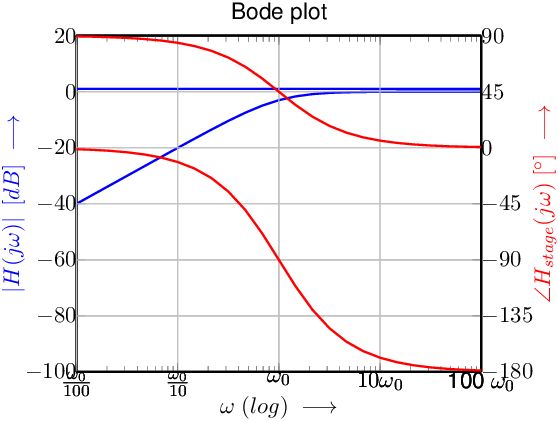
An answer:

The loop gain is $A_{\mathit{loop}}(\mathit{j\omega })=A_{\mathit{buf}}\cdot \frac{1-\mathit{j\omega RC}}{1+\mathit{j\omega RC}}\cdot \frac{1-\mathit{j\omega RC}}{1+\mathit{j\omega RC}}\cdot \frac{\mathit{j\omega RC}}{1+\mathit{j\omega RC}}$. Working on this equation can be done of course. But, the explicit hint — both of them — simplifies a lot.

Using the phases of the three stages, it follows that

• $\angle A_{\mathit{loop}}(0)=90^{\circ }$
• $\angle A_{\mathit{loop}}(\infty )=-360^{\circ }$
• the total phase shift ranges from $90^{\circ }\to -360^{\circ }$
• the phase shift (change) of the first two stages it twice that of the third stage.

It follows that for $A_{\mathit{buf}}>0$ there are two possibilities to get $\angle A_{\mathit{loop}}=N\cdot 360^{\circ }$:

• $\omega \to \infty$
• some finite $\omega$ close to the ${\omega }_0$ in the Bode plot.

There is no way to get harmonic oscillation at the finite $\omega$ solution because the $|A_{\mathit{loop}}|$ is higher at $\omega \to \infty$ and hence the solution at that $\omega \to \infty$ will win. And that’s not regarded as oscillation.

IF you would calculate the finite $\omega$ solution, then the answer would follow from having to achieve $-90^{\circ }$ phase shift in the 3 stages, resulting in respectively (symmetry!) $-90^{\circ }\ast 2∕5=-36^{\circ }$, $-90^{\circ }\ast 2∕5=-36^{\circ }$, $-90^{\circ }\ast 1∕5=-18^{\circ }$ phase shift. That would then result in ${\omega }_{\mathit{osc}}=1∕\mathit{RC}\cdot \mathit{tan}(18^{\circ })$. But, sorry, the $\omega \to \infty$ wins...

Using the other hint requires rewriting transfer functions to standard form. The three forms would then be:

$$\begin{array}{llll}\hfill & H_{1,2}(\mathit{j\omega })=\frac{1-\mathit{j\omega RC}}{1+\mathit{j\omega RC}}\to \frac{1+{(\mathit{\omega RC})}^2}{{(1+\mathit{j\omega RC})}^2}& \hfill & \\ \hfill & H_3(\mathit{j\omega })=\frac{\mathit{j\omega RC}}{1+\mathit{j\omega RC}}& \hfill & \end{array}$$

And the loop gain would then be: $A_{\mathit{loop}}(\mathit{j\omega })=A_{\mathit{buf}}\cdot \frac{1+{(\mathit{\omega RC})}^2}{{(1+\mathit{j\omega RC})}^2}\cdot \frac{1+{(\mathit{\omega RC})}^2}{{(1+\mathit{j\omega RC})}^2}\cdot \frac{\mathit{j\omega RC}}{1+\mathit{j\omega RC}}$ which has an imaginary numerator and a complex denominator. This enables relatively easy solving, leading to the exact same findings as before.

(f)

An answer:

The same analyses as for the previous question can be used.

Using the phases of the three stages and including the $\pm 180^{\circ }$ of $A_{\mathit{buf}}$, it follows that

• $\angle A_{\mathit{loop}}(0)=270^{\circ }$
• $\angle A_{\mathit{loop}}(\infty )=-180^{\circ }$
• the total phase shift ranges from $270^{\circ }\to -180^{\circ }$
• the phase shift (change) of the first two stages it twice that of the third stage.

It follows that for $A_{\mathit{buf}}<0$ there is only one possibility to get $\angle A_{\mathit{loop}}=N\cdot 360^{\circ }$:

• some finite $\omega$ close to the ${\omega }_0$ in the Bode plot.

For this solution, the 3 stages combined have to achieve $-270^{\circ }$ phase shift, resulting in respectively (symmetry!) $-270^{\circ }\ast 2∕5=-108^{\circ }$, $-270^{\circ }\ast 2∕5=-108^{\circ }$, $-270^{\circ }\ast 1∕5=-54^{\circ }$ phase shift. That would then result in ${\omega }_{\mathit{osc}}=1∕\mathit{RC}\cdot \mathit{tan}(54^{\circ })$. $A_{\mathit{buf}}$ then follows from equating $A_{\mathit{loop}}(j{\omega }_{\mathit{osc}})=1$