Exercise 7.5 Stability and phase marging

a)

An answer:
Assuming stable behavior, for an ideal opamp $v_{+}=v_{-}$ which yields directly $$\begin{array}{rcll}& & V_{\mathit{REF}}=\frac{R_1}{R_1+R_2}{v}_{\mathit{OUT}}& \\ & & v_{\mathit{OUT}}=\left(1+R_2∕R_1\right)V_{\mathit{REF}}& \end{array}$$

b)

An answer:
At the unity-gain frequency, the modulus of the gain is 1 by definition, leading to $$\begin{array}{rcll}& A(\mathit{j\omega })& =\left|\frac{A_0}{(1+\mathit{j\omega \tau })}\right|\equiv 1& \\ & & \Rightarrow & \\ & & |1+\mathit{j\omega \tau }|=A_0& \\ & & \Rightarrow & \\ & & A_0=\sqrt{1^2+{\omega }^2{\tau }^2}& \\ & & \Rightarrow & \\ & & f=\frac{1}{2\pi }\sqrt{\frac{A_0-1}{{\tau }^2}}\approx \frac{A_0}{2\mathit{\pi \tau }}& \end{array}$$

Another approach is by drawing a Bode plot. Asymptotically, the (angular) corner frequency lies at $1∕\tau$ at a gain of $A_0$, and rolls-off first order for higher frequencies. It crosses the zero dB axis if the (modulus of the) gain is reduced by a factor $A_0$. Being a first order system that must be at a frequency factor of $A_0$ higher than the corner frequency.

c)

An answer:
The loop consists of (in arbitrary order):

• the transistor, which translates into a transconductance $g_m$ for small signals
• the resistive divider with $C_{\mathit{out}}$
• the opamp (via the non-inverting input

The loop gain is then

$$\begin{array}{rcll}& A_{\mathit{loop}}& =-g_m\cdot \frac{R_1+R_2}{1+\mathit{j\omega }(R_1+R_2)C_{\mathit{out}}}\cdot \frac{R_1}{R_1+R_2}\cdot \frac{A_0}{1+\mathit{j\omega \tau }}& \\ & & =-g_m{R}_1{A}_0\cdot \frac{1}{1+\mathit{j\omega }(R_1+R_2)C_0}\cdot \frac{1}{1+\mathit{j\omega \tau }}& \end{array}$$

d)

An answer:
It was stated that the unloaded regulator is stable, with a sufficient phase margin. Furthermore the loop gain at DC is probably much larger than unity because $A_0>>1$. This implies that the (magnitude part of the) Bode plot of $A_{\mathit{loop}}$ is as shown below:

• $A_{\mathit{loop}}(0)>>0$
• there are two poles, where the second one is located at frequencies where $|A_{\mathit{loop}}|<1$ (for sufficient phase margin)

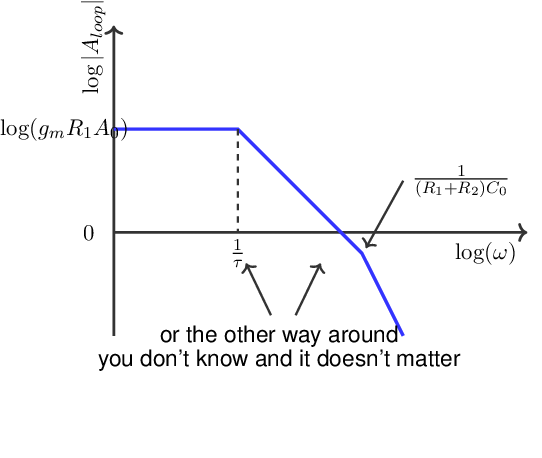
A higher $I_{\mathit{OUT}}$ increases the $g_m$ of the transistor. That shifts the curve in the Bode plot upwards, which decreases the phase margin.