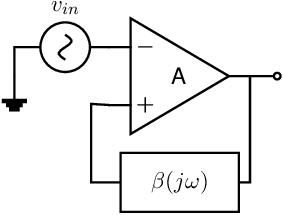
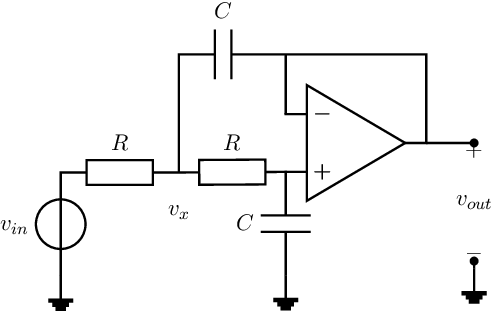
Show that the transfer function of this filter is for .
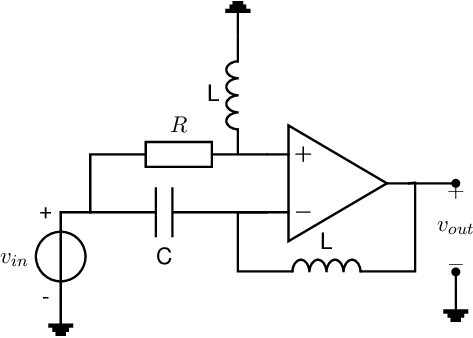
Show that the transfer function of this filter is .
Now we want to see if it is possible to make a harmonic oscillator if we connect the low-pass filter from above in series with a voltage buffer and a couple of other opamp circuits in a closed-loop, see the circuit diagram below. The opamps are ideal, with a real valued . The voltage gain of the voltage buffer at the top of the schematic is a real valued negative factor .
Note that the value of all resistors is the same (R), that the capacitors have identical values (C), and that all inductors have identical values (L).
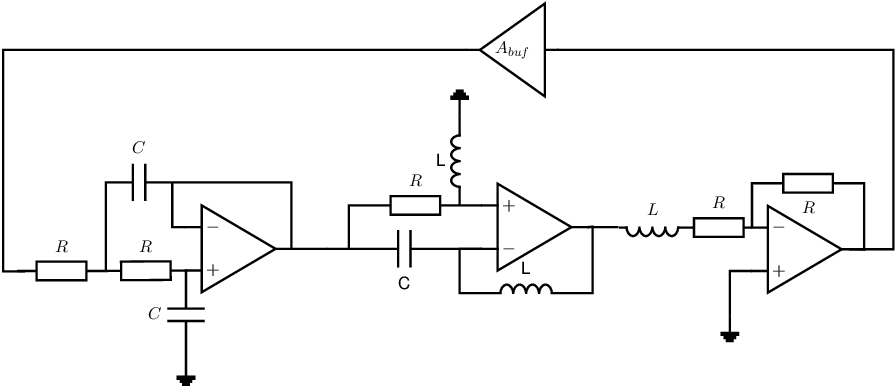
Derive the transfer function for every stage.