An answer:
makes sure that there is zero DC-current in ,
and that hence
does not influence the bias point
An answer:
An answer:
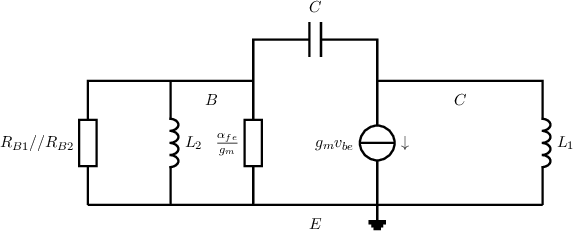
An answer:
with
where . This leads to
Collecting the imaginary terms and equating them to zero yields
yielding the oscillation (radian) frequency
An answer:
Equating the loop gain, at the oscillation frequency, and equating that to 1 gives