[next] [tail] [up]

Exercise 10.1 A Colpitts oscillator

a)


An answer:

pict

b)


An answer:
The loop gain equals 1; this is used in the derivations below.

c)


An answer:
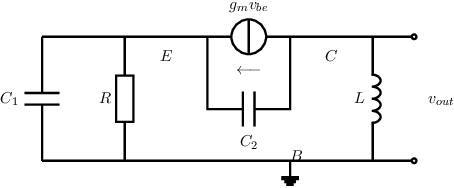
The loop gain equals 1 at the oscillation frequency. This oscillation frequency follows from equating the loop gain to a real value. To derive the loop gain: the best way is to cut the loop inside an abstract controlled block. In this schematic the only abstract controlled block is the SSEC of the transistor.

Aloop = V B − V E vbe = −vE vbe vE = iE ⋅ ZA(defining ZA = Zc1∕∕R) iE = gm ⋅ vbe + vout − vE ZC2 vout = −iEZL iE = gm ⋅ vbe −iEZL ZC2 − vE ZC2 = gm ⋅ vbe − vE ZC2 1 + ZL ZC2 = gm ⋅ vbeZC2 − vE ZC2 + ZL vE = (gm ⋅ vbeZC2 − vE ZC2 + ZL ) ⋅ ZA = gm ⋅ vbeZC2 ZC2 + ZL ⋅ ZA − vE ZC2 + ZL ⋅ ZA = gm ⋅ vbeZC2 ZC2 + ZL ⋅ ZA 1 + ZA ZC2+ZL = vbe ⋅ gm ⋅ ZAZC2 ZC2 + ZL + ZA Aloop = − gm ⋅ ZAZC2 ZC2 + ZL + ZA

At oscillation, this Aloop ≡ 1 which can be expanded as e.g.:

−gm ⋅ Zc1R Zc1+RZC2 = ZC2 + ZL + Zc1R Zc1 + R −gm ⋅ R 1+jωRC1 ⋅ 1 jωC2 = 1 jωC2 + jωL + R 1 + jωRC1 −gm ⋅ R = (1 + jωRC1) + jωL ⋅ (1 + jωRC1) ⋅ (jωC2) + R ⋅ (jωC2)

Collecting the imaginary terms and equating these to zero yield

ωosc2 = C1 + C2 C1C2L → ωosc = C1 + C2 C1C2L

d)


An answer:
Recycling the previously found equations for loop gain, and equating that to 1 at ω = ωosc (note that this implies that you only have to take the real terms into account) this yields:

gmR = ωosc2C 1L − 1 → gm = C1 RC2

[next] [front] [up]