An answer:
The closed-loop transfer is . For , , hence a sine would be sustained indefinitely without any input signal. This is harmonic oscillation, with in equation .
An answer:
The derivation of can be done in many ways. One of these is shown below.
after which can be calculated in a variety of ways. E.g. applying KCL on node gives:
Rewriting into and using that along with yields
An answer:
One of the many correct derivation of
is shown below.
Yielding
An answer:
An answer:
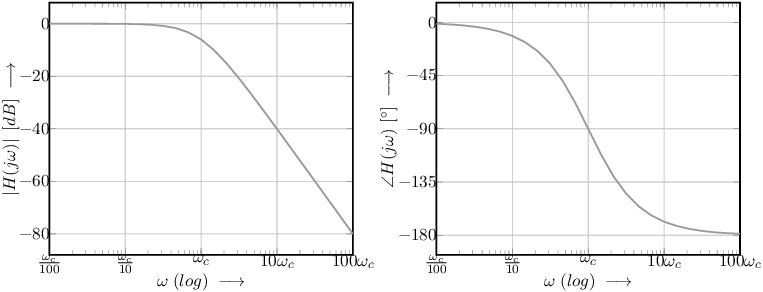
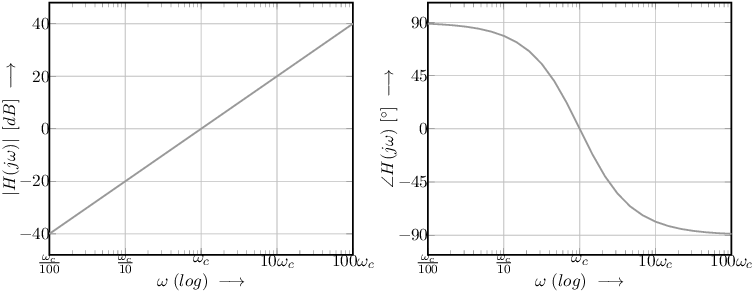
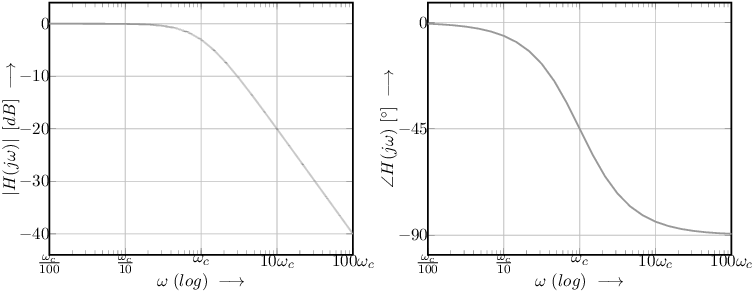
An answer:
The open-loop transfer function is:
Assuming the same corner frequencies for the sections,
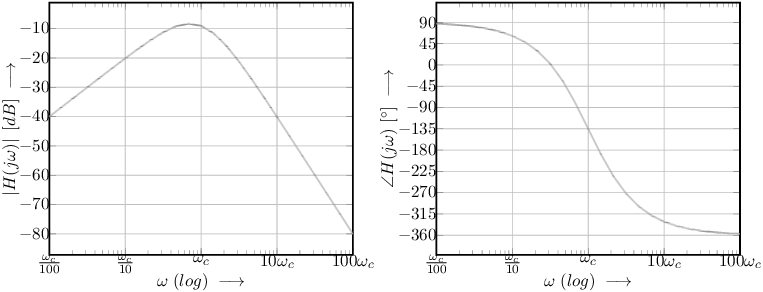
An answer:
yes.
An answer:
yes.