Exercise 9.10 An harmonic oscillator with RL and RC sections

(a)

(b)

An answer:
$$\begin{array}{llll}\hfill & H_1(\mathit{j\omega })=A_v\cdot \frac{\mathit{j\omega L}∕R}{1+\mathit{j\omega L}∕R}& \hfill & \\ \hfill & H_2(\mathit{j\omega })=\frac{\mathit{j\omega L}∕R}{1+\mathit{j\omega L}∕R}& \hfill & \\ \hfill & H_3(\mathit{j\omega })=\frac{1}{1+\mathit{j\omega RC}}& \hfill & \\ \hfill & H_4(\mathit{j\omega })=1& \hfill & \\ \hfill & & \hfill \end{array}$$

(c)

An answer:

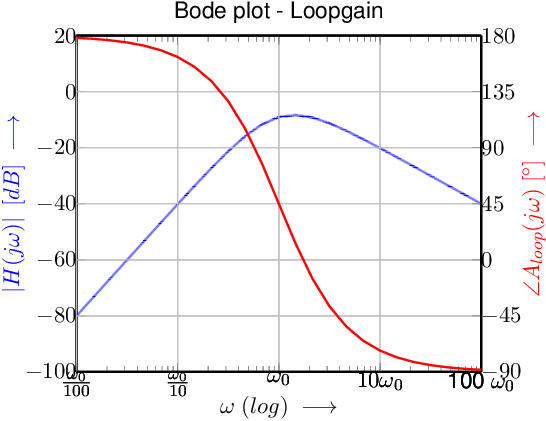
For these plots, ${\omega }_0=1$. Asymptotic the $|H(j{\omega }_0)|=1=0\mathit{dB}$.

(d)

An answer:
This loopgain has $180^{\circ }$ phase shift at $\omega =0$ and has $-90^{\circ }$ phase shift at $\omega \to \infty$. Somewhere in the middle, close to ${\omega }_0$, the phase shift of the loopgain is $0^{\circ }$. Using a well selected $A_v>1$ the circuit can oscillate harmonically.

(e)

An answer:
$$\begin{array}{llll}\hfill H_{\mathit{loop}}(\mathit{j\omega })& =A_v\cdot \frac{\mathit{j\omega L}∕R}{1+\mathit{j\omega L}∕R}\cdot \frac{\mathit{j\omega L}∕R}{1+\mathit{j\omega L}∕R}\cdot \frac{1}{1+\mathit{j\omega RC}}& \hfill & \\ \hfill & =A_v\cdot \frac{(\mathit{j\omega L}∕R)\cdot (\mathit{j\omega L}∕R)}{(1+\mathit{j\omega L}∕R)\cdot (1+\mathit{j\omega L}∕R)\cdot (1+\mathit{j\omega RC})}& \hfill & \end{array}$$

This has a real numerator and a complex denominator. If the denominator is real for a specific non-zero and finite $\omega$ then the circuit can oscillate harmonically.

$$\begin{array}{llll}\hfill H_{\mathit{loop}}(\mathit{j\omega })& =A_v\cdot \frac{(\mathit{j\omega L}∕R)\cdot (\mathit{j\omega L}∕R)}{1+\mathit{j\omega }(2L∕R+\mathit{RC})+j^2{\omega }^2(2L^2∕R^2+\mathit{LC})+j^3{\omega }^3{L}^{2}C∕R}& \hfill & \end{array}$$

This is obviously possible for the derived loopgain.

(f)

An answer:
$$\begin{array}{llll}\hfill & \mathit{j\omega }(2L∕R+\mathit{RC})+j^3{\omega }^3{L}^{2}C∕R=0\to & \hfill & \\ \hfill & {\omega }_{\mathit{osc}}=0(\mathrm{\text{no oscillation}})& \hfill & \\ \hfill & {\omega }_{\mathit{osc}}^2=\frac{2L∕R+\mathit{RC}}{L^{2}C∕R}(\mathrm{\text{can oscillate}})& \hfill & \end{array}$$

Substitute this in the next equation to get the required value of $A_v$:

$$\begin{array}{llll}\hfill A_v& =\frac{{\omega }_{\mathit{osc}}^2(2L^2∕R^2+\mathit{LC})-1}{({\omega }_{\mathit{osc}}L∕R)\cdot ({\omega }_{\mathit{osc}}L∕R)}& \hfill & \end{array}$$

(g)

An answer:
Not applicable.