Exercise 7.3 Phase margins

a)

An answer:
A straight forward derivation (using e.g. $v_{-}=v_{+}$ which holds for stable systems with $A\to \infty$) yields

$H(\mathit{j\omega })=\frac{v_{\mathit{out}}}{v_{\mathit{in}}}=\frac{R_2+Z_{L1}}{R2}=1+\frac{\mathit{j\omega }{L}_1}{R_2}$

Note that this yields some kind of high-pass characteristic.

b)

An answer:

$$\begin{array}{rcll}& H(\mathit{j\omega })& =\frac{v_{\mathit{out}}}{v_{\mathit{in}}}& \\ & & v_{\mathit{out}}=A\left(v_{\mathit{in}}-\frac{R_2}{R_2+\mathit{j\omega }{L}_1}{v}_{\mathit{out}}\right)& \\ & & =A\cdot v_{\mathit{in}}\frac{1}{\left(1+\frac{A}{1+\mathit{j\omega }{L}_1∕R_2}\right)}& \\ & H(\mathit{j\omega })& =\frac{A}{1+\frac{A}{1+\mathit{j\omega }{L}_1∕R_2}}& \end{array}$$

For a Bode plot, rewriting into a standard form is the easiest. The pole(s) and zero(s) and (here) the DC-voltage gain follow directly.

$$\begin{array}{rcll}& H(\mathit{j\omega })& =\frac{A}{1+\frac{A}{1+\mathit{j\omega }{L}_1∕R_2}}& \\ & & =\frac{A\left(1+\mathit{j\omega }{L}_1∕R_2\right)}{1+A+\mathit{j\omega }{L}_1∕R_2}& \\ & & =\frac{A}{1+A}\cdot \frac{1+\mathit{j\omega }{L}_1∕R_2}{1+\mathit{j\omega }\frac{L_1∕R_2}{1+A}}& \end{array}$$

c)

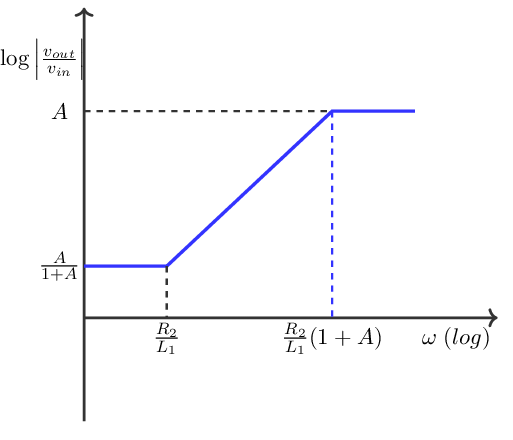
An answer:

$$\begin{array}{rcll}& A_{\mathit{loop}}(\mathit{j\omega })& =\frac{A_0}{1+\mathit{j\omega }∕{\omega }_1}\cdot \frac{1}{1+\mathit{j\omega }{L}_1∕R_2}& \end{array}$$

Conclusion: at the second pole ($f=\frac{10^6}{2\pi }$) the phase shift of the loopgain is $-135°$. At the frequency where the loopgain equals 1, the phase margin is larger than $45°$.