Exercise 9.9 An harmonic oscillator?

Given is the circuit below; this circuit is intended to be an harmonic oscillator.

• The opamps are ideal, with a real valued voltage gain $A\to \infty$ and with no frequency dependency.
• The voltage gain of the voltage buffer at the top of the schematic is a real valued factor $A_{\mathit{buf}}$; this value can be positive or negative.
• The value of all resistors is the same (R), the capacitors have identical values (C), and all inductors have identical values (L) - this is to simplify your derivations.

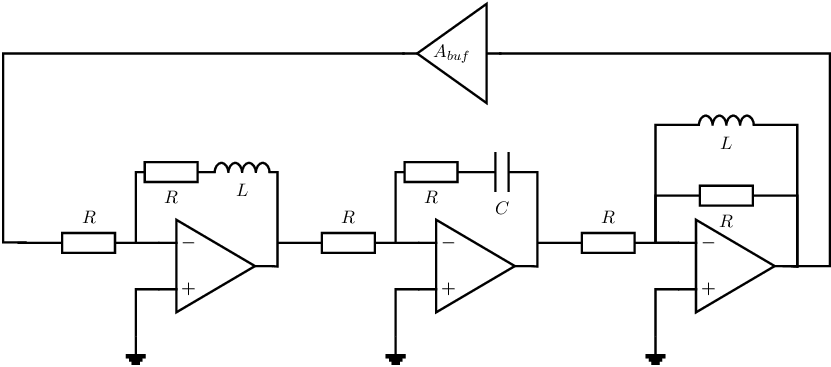
(a)

Which condition(s) must be satisfied to get harmonic oscillation?

(b)

Derive the voltage transfer for each of the 3 stages at the bottom of the figure. Each stage starts at the output node of the previous opamp/amplifier and ends at the output node of the opamp in the stage.
Combined with the $A_{\mathit{buf}}$ this forms the loop gain.

(c)

Determine whether the given circuit can function as harmonic oscillator for a specific (real) value of $A_{\mathit{buf}}$. If your answer shows that harmonic oscillation can be possible, go to question (d). Otherwise go to question (e).

(d)

IF harmonic oscillation possible at question (c): derive an equation for the oscillation frequency AND (after that) derive an equation for the required value of $A_{\mathit{buf}}$. Both these equations should be functions of the various component values in the schematic — they may be ugly equations. After finishing (d) skip (e).

(e)

IF no harmonic oscillation possible at question (c): swap a resistor and the reactive component in one of the stages in such a way that harmonic oscillation can be achieved, and then redo questions (c) and (d). IF there is no way to get the circuit to oscillate harmonically: prove that!